Визуализация Contour Plot и ее частный случай Tanaka Contours для Tableau вещь довольно экзотическая. Визуализации такого типа встречаются в спортивном анализе и гео-анализе. В спортивной аналитике такие визы встречаются у довольно известного дата-журналиста Kirk Goldsberry. Например, мне нравятся его работы в статьях ESPN:
Seven ways the NBA has changed since Michael Jordan’s Bulls
Why Michael Jordan’s scoring prowess still can’t be touched
И пара таких типов визуализаций в QGIS:
How to create illuminated contours, Tanaka-style
Tanaka method or how to make shaded contour lines
Есть примеры Contour Plot на Tableau Public:
Anthony Bourdain’s most visited places in the world, автор Sebastián Soto Vera
Game of Thrones: a study of the main characters, автор Nico Cirone
Contour plot вы могли видеть на синоптических картах, где изобарами и изохорами показывают давление и температуру. Также такие контуры можно встретить на картах рельефа, где ими отображают высоту местности или глубину водоемов. В этой статье при помощи контуров мы будем показывать плотность каких-либо событий на участке местности, а точнее, распределение вероятностей событий. Нашей задачей дальше будет визуализация успешных бросков разных игроков НБА таким образом, чтобы понять с каких точек больше забрасывает тот или иной игрок. То есть, исходя из первичных координат бросков на площадке, мы опишем функцию распределения вероятностей того, что игрок забросит мяч с конкретной точки.
Этой статьи не было бы без проекта SportsVizSunday и Zak Geis, который собрал всю статистику бросков игроков НБА с координатами на площадке в один датасет, а также сделал прекрасный виз, в котором есть много интересных фишек, и его интересно смотреть не только фанатам НБА. Мои две визуализации ‘NBA Hot Spots’ для проекта SportsVizSunday, JUNE 2020 — NBA SHOT LOCATIONS показывают ‘горячие точки’ бросков на баскетбольной площадке известных баскетболистов NBA:
В этой статье рассмотрим как строить такие визуализации, будем использовать тот же самый дата сет.
1. Density map in Tableau
Для того, чтобы лучше понять как работают Contour Plots, рассмотрим как нативные Density Marks показывают плотность бросков на площадке. Большинство успешных бросков проходят из-под кольца, мы же рассмотрим паттерны игроков с бросками от 8 футов и выше, но при этом исключим дальние броски с другой половины площадки — их очень мало, и они не отражают игру на половине поля противника. Для этого отфильтруем броски по полю Shot Zone Range, отбросив категории Less Than 8 ft. и Back Court Shot. Отфильтруем только успешные броски – Shot Made Flag =1. Возьмем самого известного игрока НБА, номера 1 по разным версиям, Майкла Джордана – поле Player Name – Michael Jordan. Построим диаграмму разброса, используя в качестве подложки изображение площадки: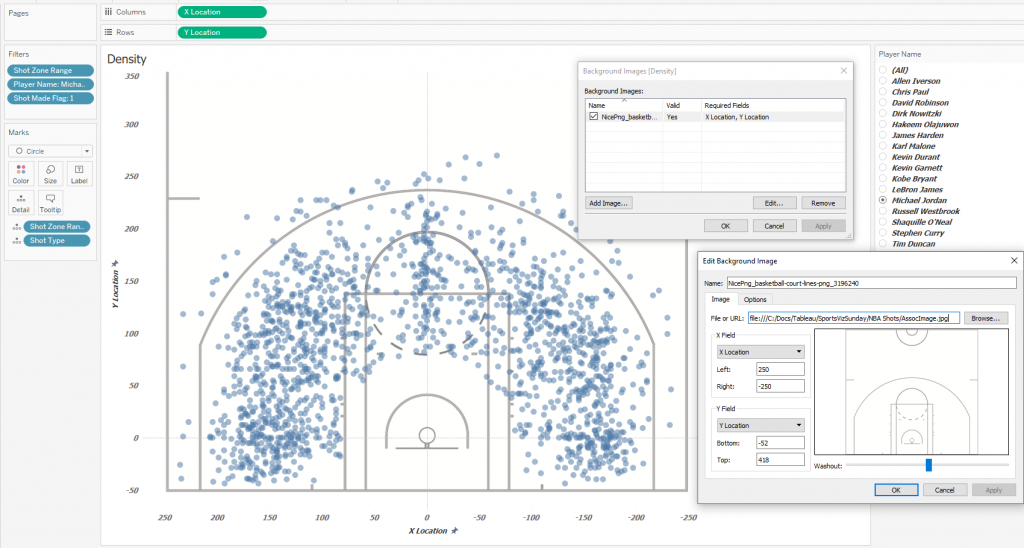 
Эта диаграмма дает представление о том, откуда чаще всего забрасывал Майкл Джордан, но проблема заключается в том, что на одной паре координат может находиться много точек, и сложно представить насколько плотно лежат точки даже если сделать их полупрозрачными. Для большего понимания распределений, построим распределения бросков по оси X и оси Y площадки. Сделаем bins c размером 5 для X и для Y, чтобы немного сгладить неровности распределений. Для оси X это выглядит так: 
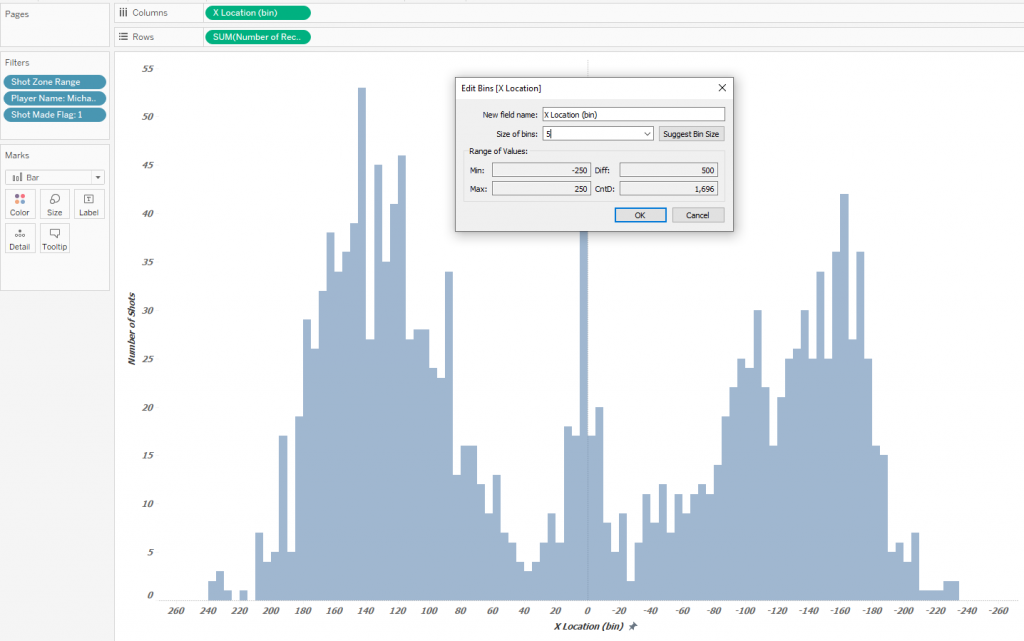Теперь распределения по оси X и по оси Y представим на одном дашборде, а также в диаграмме разброса поменяем метки на Density: 
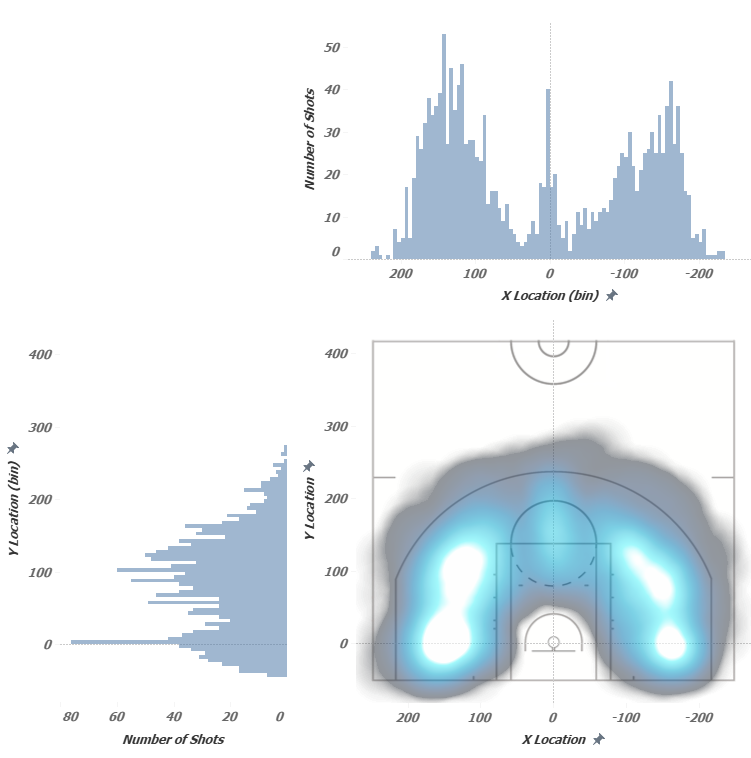Эта картинка намного лучше дает представление о плотности бросков – сразу видны места их скоплений. Также надо заметить, что при использовании Density Map показываются не сами точки бросков, а некоторая трехмерная функция заполняет пространство между точками, показывая цветом по оси Z концентрацию этих бросков, то есть, на рисунке представлены не data points. В Contour Plots сами data points тоже не показываются – есть только контуры, показывающие эквивалентные значения величин, то есть, непрерывная функция распределения разбивается на уровни. Для нахождения контуров и описывающих их точек воспользуемся скриптом на Python
2. Kernel Density Estimation в Python
В Python есть возможность расчета и визуализации контуров. Скрипт ниже позволяет генерировать набор координат точек контуров, посмотреть сами контуры и выгрузить координаты в .csv. Можно оценить плотность распределения по двум координатам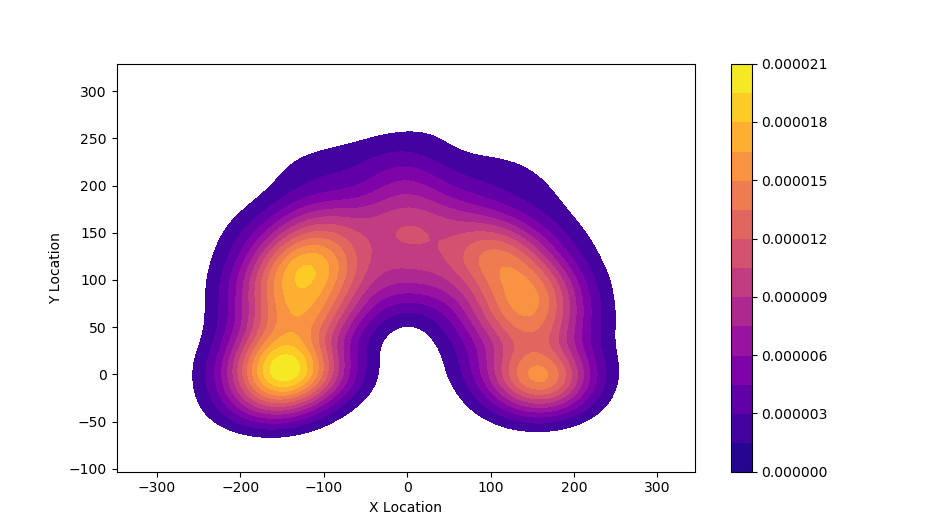
A также по каждой из координат отдельно: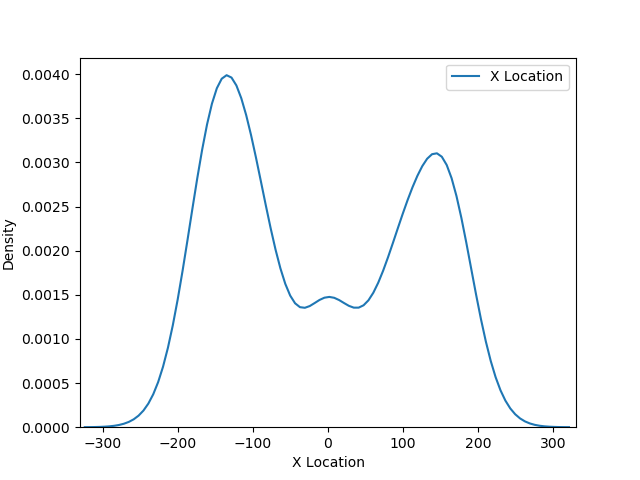 
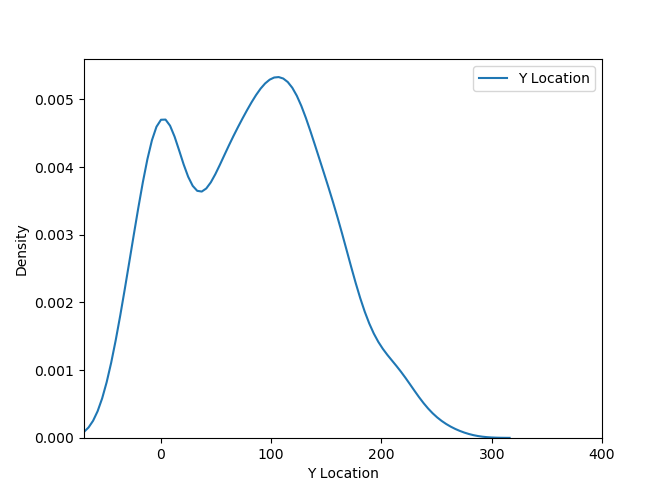
Если поместить эти графики на одну картинку, получим представление о распределении плотности событий (успешных бросков)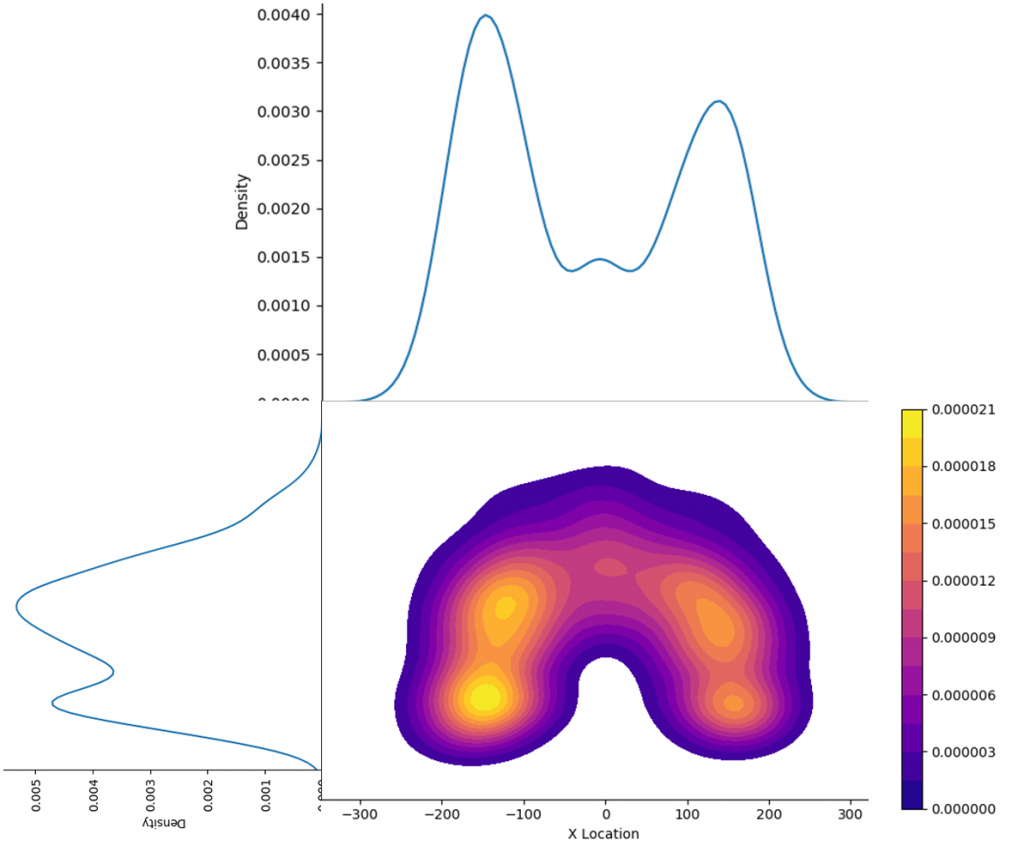 
Давайте разберемся что означают эти графики. Здесь используется алгоритм ядерной оценки плотности или Kernel Density Estimation, KDE. Этот метод сглаживает данные.
Можно сравнить распределения, построенные в Табло (уже частично сглаженные группировкой в bins) и кривые, полученные при помощи Python. Сам метод позволяет оценить распределение событий, описывая имеющуюся выборку данных. В нашем случае выборка – это броски Джордана. Но точки бросков не покрывают всю зону площадки, а метод KDE достраивает поверхность распределения во всех точках. Эта поверхность распределения делится на уровни равными величинами по оси Z. Уровни обозначаются цветами и отображаются в легенде.
Теперь давайте разберемся что означают числа в легенде Contour Plot и значения Density на графиках. Эти числа обозначают вероятности возникновения события в конкретной точке. Их можно выражать в процентах. Площади под кривыми и объем под поверхностью распределения равны 1 или 100%. Вероятности возникновения событий при большом количестве известных событий можно расценивать как плотность (Density) событий – чем больше плотность прошедших событий, тем больше вероятность возникновения события в будущем. Таким образом, при большом количестве событий метод KDE позволяет построить поверхность распределения вероятностей, описывающую плотность возникновения событий.
3. Подготовка данных в Python
В этом разделе разберемся как загрузить определенный блок данных в Python, построить контуры распределения и выгрузить координаты конуров в .csv. Следующий код код рассчитывает и отображает контуры, их координаты и сохраняет координаты в файл:
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pylab as plt
from matplotlib.colors import rgb2hex
import sys
np.set_printoptions(threshold=sys.maxsize)
#Чтение данных из файла
data = pd.read_csv ('C:/Docs/Tableau/SportsVizSunday/NBA Shots/Output.csv')
#Выбор данных по критериям
data = data.loc[(data['Shot Zone Range'] != "Less Than 8 ft.") &
(data['Shot Zone Range'] != "Back Court Shot") &
(data['Player Name'] == "Michael Jordan")]
#Создание переменных для координат X,Y
x = -data['X Location']
y = data['Y Location']
#Задаем параметры построения Contour Plot
cs = sns.kdeplot(x, y, legend=True, shade=False, shade_lowest=False, cbar=True, gridsize=200, n_levels=15, cmap='plasma')
#Задаем пределы отрисовки диаграммы на координатной плоскости и строим диаграмму
plt.xlim(-330, 330)
plt.ylim(-70, 400)
plt.axis('on')
plt.show()
#Создаем список всех вершин, их цвет и принадлежность к контурам lines = []
vertice_id=0
path_id=0
for collection in cs.collections:
color = collection.get_edgecolor()
for path in collection.get_paths():
for vertice in path.to_polygons():
path_id = path_id + 1
for i in vertice:
vertice_id = vertice_id + 1
aa = rgb2hex(color[0]), path_id, vertice_id, i[0],i[1]
lines.append(aa)
print (rgb2hex(color[0]), path_id, vertice_id, i[0],i[1])
#Сохраняем значения в файл
np.savetxt("C:/Docs/Tableau/SportsVizSunday/NBA Shots/Michael_Jordan_Shots.csv", lines, header='color,contour_id,vertice_id,x,y', fmt='%s', delimiter=",")
В результате выполнения кода получится следующая диаграмма: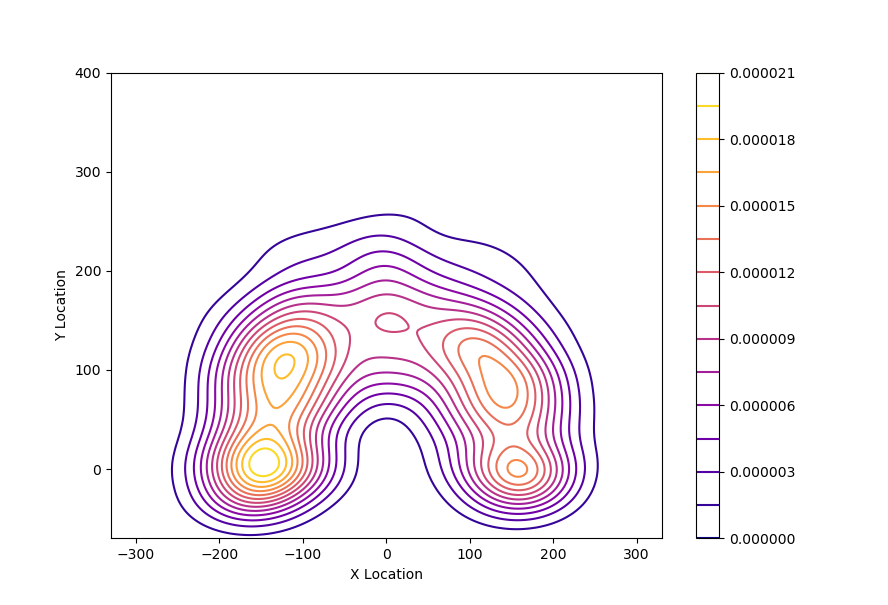
В этом коде особое внимание надо обратить на строку:
cs = sns.kdeplot(x, y, legend=True, shade=False, shade_lowest=False, cbar=True, gridsize=200, n_levels=15, cmap='plasma')
В этой строке определяются параметры для расчета и вида Contour Plot:
legend=True – отображает легенду на диаграмме, на данные не влияет
shade=False – отображает контуры без заполнения. Значение True вернет залитые контуры, как в предыдущем рисунке. В этом случае в данные выгрузятся внешние и внутренние точки контуров. Для уменьшения общего количества точек на диаграмме в Tableau, значение этого параметра установим в False
shade_lowest=True – показывает нижний или нулевой уровень при shade=True. Уровень нулевой вероятности нет смысла показывать – он займет все оставшееся пространство диаграммы, поэтому используем False
gridsize=200 – задает сетку построения диаграммы. Чем больше это число, тем более детализирована будет диаграмма, и в файл выгрузится больше точек. При gridsize=20 получим следующее: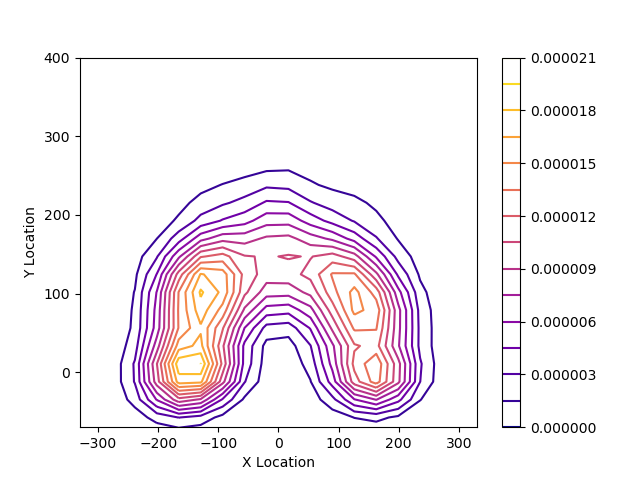
n_levels=15 – задает количество уровней в диаграмме. В нашем случае – 15 уровней. При n_levels = 5 получим следующую диаграмму:
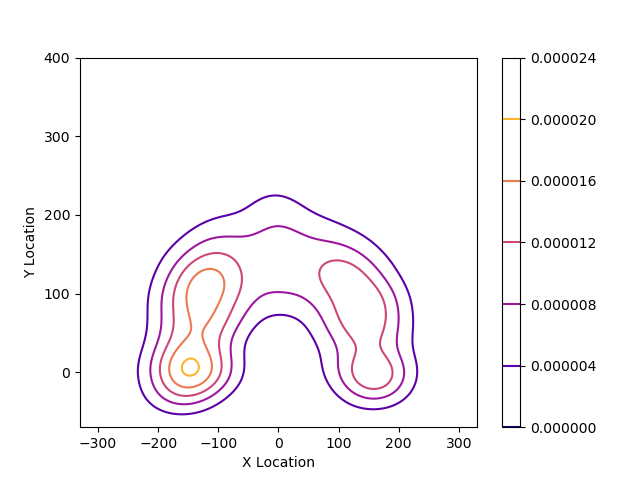
cbar=True – показывает легенду, на данные не влияет
cmap=‘plasma’ – задает цветовую палитру диаграммы, цвета которой в HEX формате выгружаются в файл. Можно выбрать другие палитры. Посмотреть все палитры можно здeсь: Вот вариант при cmap= ‘gist_ncar’
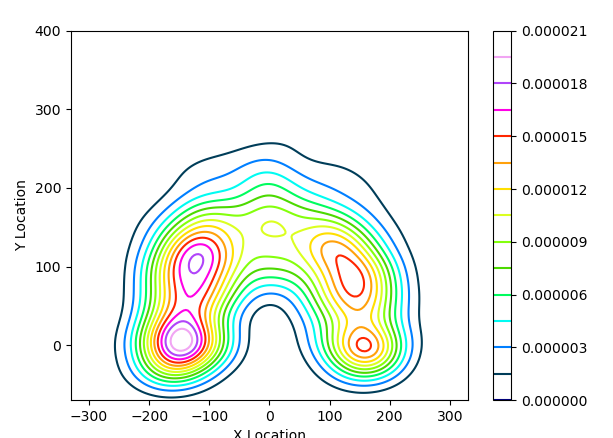
Полученный в результате выполнения кода файл .csv выглядит так:
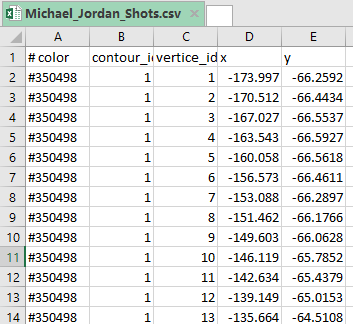
color – цвет контура
contour_id – id контура
vertice_id – id вершины
x,y – координаты вершины
4. Построение контуров в Tableau
Подключим файл .csv к Tableau и построим контуры:
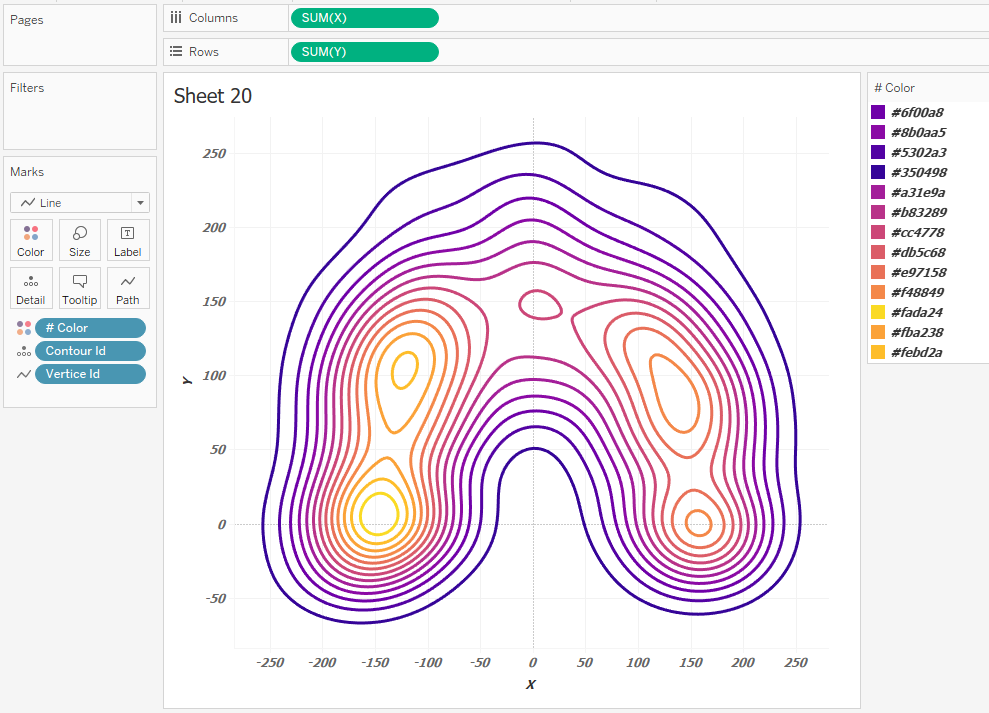
Цвет этих контуров определяется HEX форматом, вводим цвета в настройках цвета # Color на полке Marks. Переключим Marks c Lines на Polygons и зададим порядок отрисовки контуров, то есть, Z-order. Для этого настроим сортировку контуров по id контура:
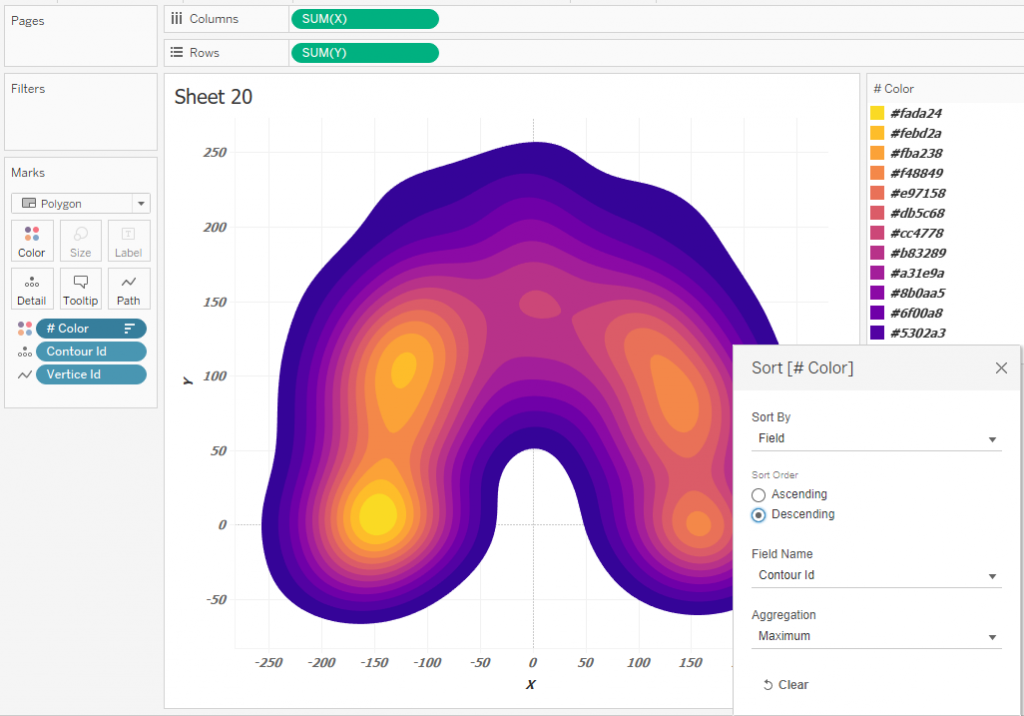
Если нужно использовать палитру из Preferences Tableau, можно цвет определять полем Continious INDEX() и настроить направление вычислений как на рисунке внизу:
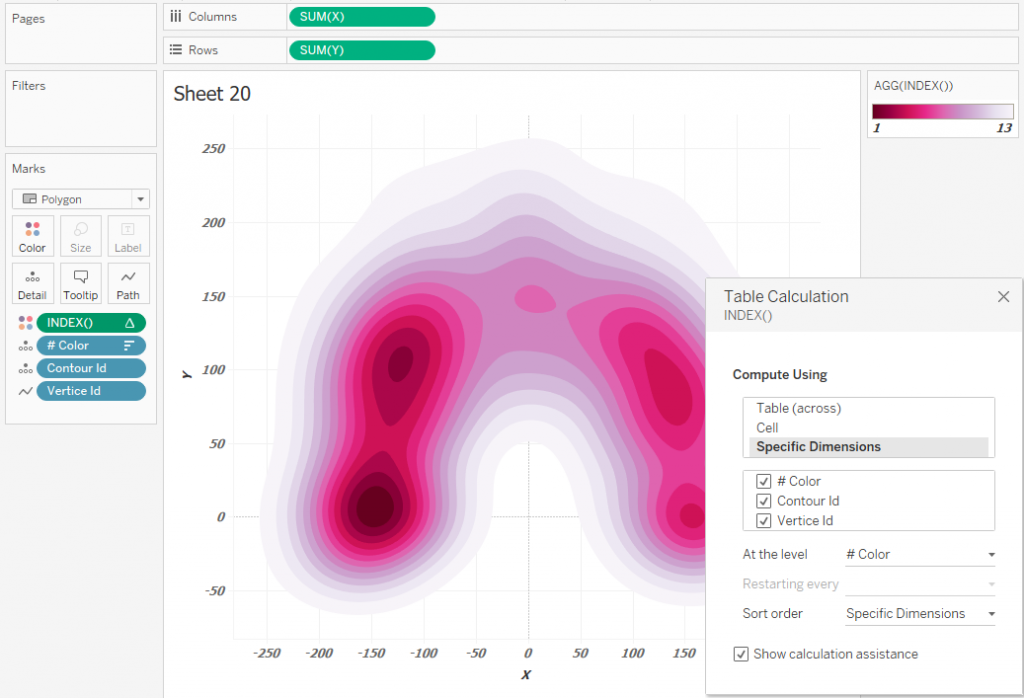
Таким образом можно построить простые Contour Plots.
5. Tanaka Contours в Tableau
Для того, чтобы получить tanaka contours, нужно добавить псевдо 3D эффект, чтобы контуры с высокой вероятностью событий казались выше. Для этого в данных сделаем UNION:
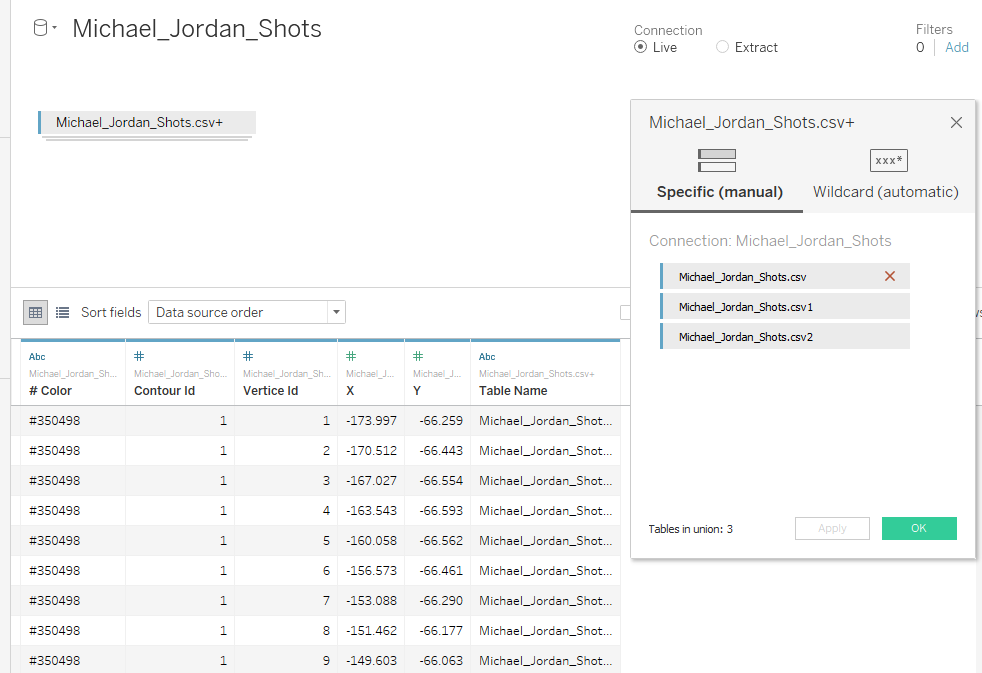
Это увеличит данные в 3 раза.
Таблица Michael_Jordan_Shots.csv будет описывать исходные контуры,
таблица Michael_Jordan_Shots.csv1 будет описывать светлые участки контуров,
таблица Michael_Jordan_Shots.csv2 будет описывать тени контуров.
Сделаем вычисление 3D Color:
CASE [Table Name]
WHEN ‘Michael_Jordan_Shots.csv’ THEN [# Color]
WHEN ‘Michael_Jordan_Shots.csv’ THEN ‘#ffffff’
WHEN ‘Michael_Jordan_Shots.csv’ THEN ‘#000000’
END
‘#ffffff’ – это HEX код белого цвета, а ‘#000000’ – черного.
Далее сделаем вычисления для новых координат. Вычисление XX:
CASE [3D color]
WHEN ‘#ffffff’ THEN [X]-1
WHEN ‘#000000’ THEN [X]+2
ELSE [X] END
Вычисление YY:
CASE [3D color]
WHEN ‘#ffffff’ THEN [Y]+1
WHEN ‘#000000’ THEN [Y]-2
ELSE [Y]
END
Из вычислений видно, что светлые участки сдвигаются на 1 по оси X и Y, а тени сдвигаются на 2 единицы по X и Y. Теперь можно нарисовать Tanaka Contours:
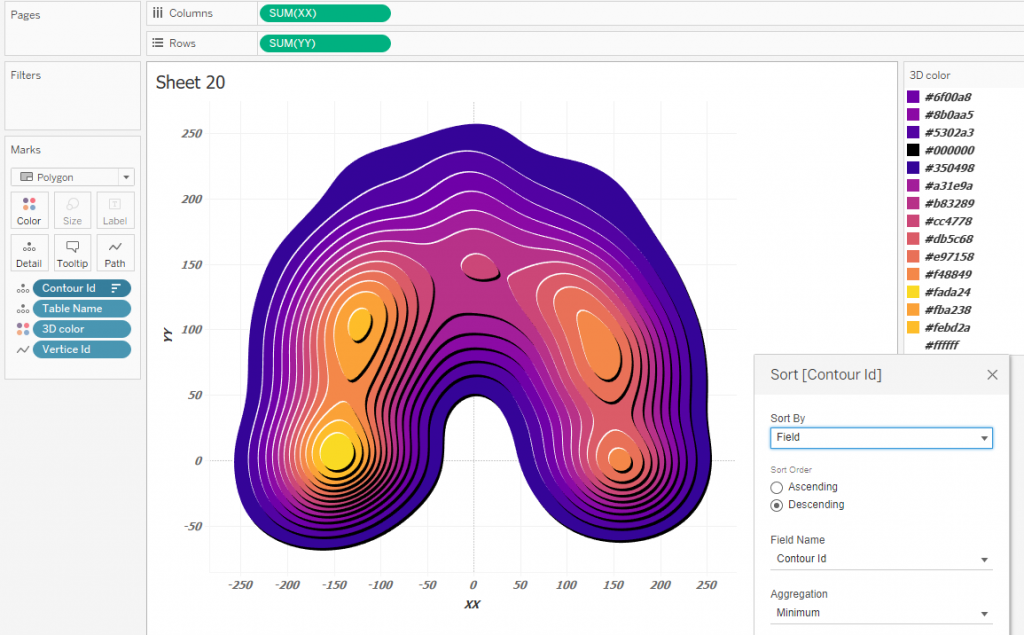
Здесь хорошо видно, что светлые контуры визуально выше темных – это как раз и есть псевдо 3D эффект. Направление теней и их ширины можно задавать, меняя величины сдвигов черных и белых полигонов в XX и YY.
Нужно обратить внимание на то, как сортируются слои. Contour_id сортируется по убыванию id, то есть, выше будут находиться контуры, описывающие бОльшую плотность. Поскольку в грануляции находится еще Table Name, то слои сортируются по id и по Table Name внутри каждого id. Таким образом, Z-order будет таким: id_10 c данными, id_10 белый, id_10 черный … id_1 c данными, id_1 белый, id_1 черный. Такая сортировка и позволяет воспринимать диаграмму как объемную с тенями.
Для большего понимания сортировки контуров посмотрите на рисунок внизу, где показан трехмерный вид и нагляден порядок сортировки по оси Z.
Внимание: Z-order — это важная метрика, определяющая порядок перекрытия двумерных объектов. Более подробно я писал про нее в статье «3D модели в Tableau«.
Мы научились строить простые Contour Plots. Дальше рассмотрим проблему мультиполигонов.
6. Работа с мультиполигонами
Уровни Contour Plot не всегда определяются одним полигоном – уровень может содержать несколько полигонов, а также содержать полигоны с отверстиями. В диаграмме бросков Майкла Джордана есть уровни, содержащие несколько полигонов, но они отрисовываются независимо, поскольку в грануляции есть Contour_id. Такие случаи не искажают картину. Если же контур содержит отверстия, то он может неправильно отрисовываться, и нужно это исправить.
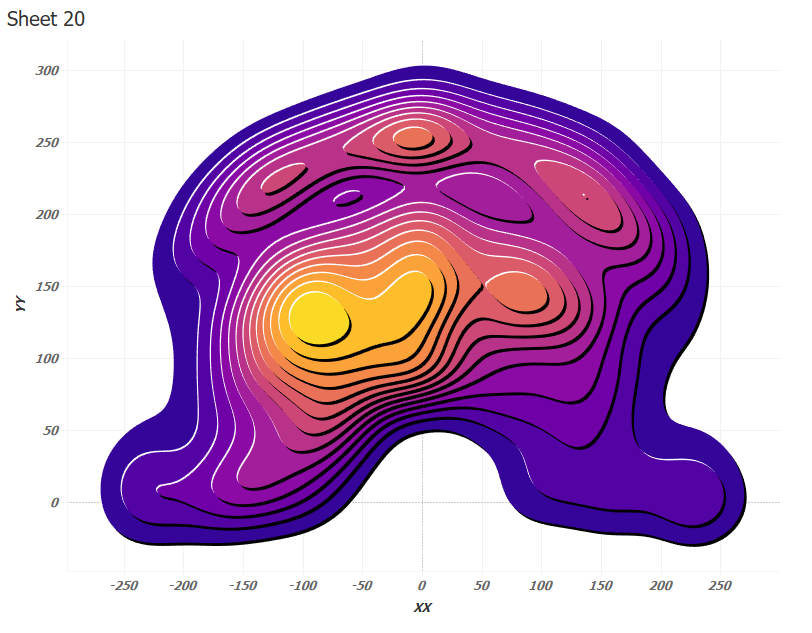Выше середины диаграммы есть два контура (Contour Id 5 и 7) того же цвета, что и контуры выше которых они находятся. Для них нужно взять цвет на уровень ниже в вычислении 3D Color:
CASE [Table Name]
WHEN ‘Michael_Jordan_Shots.csv’ THEN IF [Contour Id]=5 THEN ‘#6f00a8’ ELSEIF [Contour Id]=7 THEN ‘#8b0aa5’ ELSE [# Color] END
WHEN ‘Michael_Jordan_Shots.csv1’ THEN ‘#ffffff’ WHEN ‘Michael_Jordan_Shots.csv2’ THEN ‘#000000’
END
А также сместить черные и белые слои в направлении, противоположном основному смещению:
XX
CASE [3D color]
WHEN ‘#ffffff’ THEN IF [Contour Id]=5 OR [Contour Id]=7 THEN [X]+1 ELSE [X]-1 END
WHEN ‘#000000’ THEN IF [Contour Id]=5 OR [Contour Id]=7 THEN [X]-2 ELSE [X]+1 END
ELSE [X]
END
YY
CASE [3D color]
WHEN ‘#ffffff’ THEN IF [Contour Id]=5 OR [Contour Id]=7 THEN [Y]-1 ELSE [Y]+1 END
WHEN ‘#000000’ THEN IF [Contour Id]=5 OR [Contour Id]=7 THEN [Y]+2 ELSE [Y]-2 END
ELSE [Y]
END
Сейчас все верно:
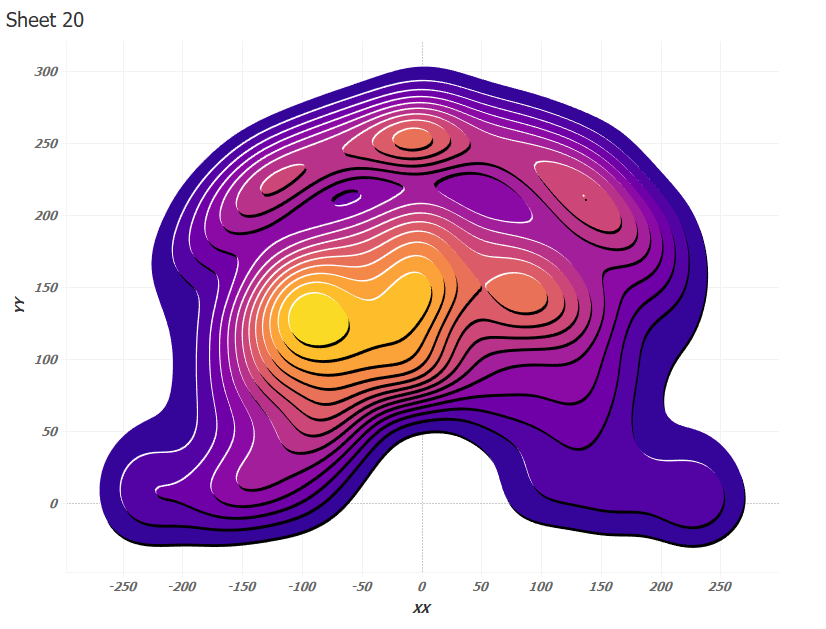
7. Пример Tanaka Contours на карте
Визуализацию, отображающую плотность преступлений в Лондоне по типам на карте, можно посмотреть по ссылке: Более полумиллиона фактов антисоциального поведения описывается диаграммой Tanaka Contours:
Довольно интересный эффект получается, если придать объем линиям контуров:
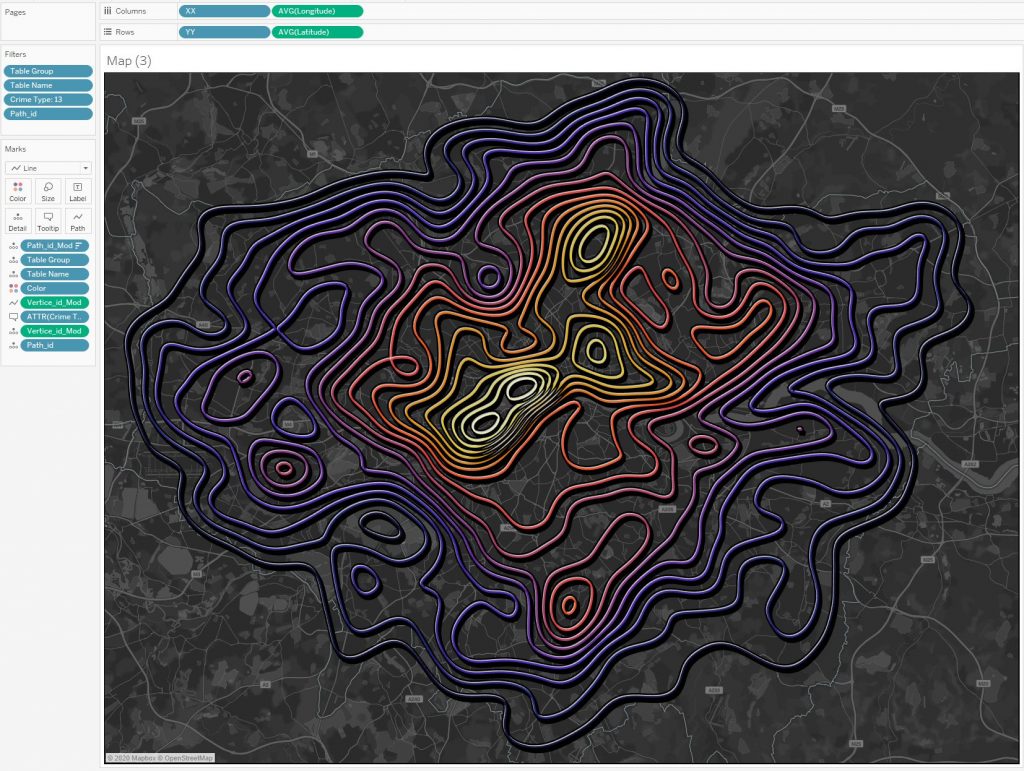
Эти визуализации помогают быстро находить места концентрации преступлений
Заключение
Contour Plots можно использовать как визуализацию концентрации каких-то событий, либо оценки вероятности наступления события в определенной точке. Такие визуализации хорошо работают на картах и в спортивной аналитике, но их можно использовать и на диаграммах разброса с большим количеством точек.