Математика прекрасна!
Цель этой статьи показать пользователям Tableau, что математика — это не только скучные числа и формулы, и что можно рисовать любые картины, описывая их математическими функциями. Ниже на картинке изображены портреты известных людей, нарисованные математическими функциями в Tableau. Сложно представить, но в датасете этой визуализации всего два числа: 0 и 500. Кривые, образующие портреты описываются параметрическими уравнениями для осей X и Y.
Клик на картинке откроет визуализацию:

Ken Flerlage написал прекрасный пост про параметрические уравнения и их использование в Tableau.
Вы можете прочитать этот пост, если хотите узнать больше про параметрические уравнения, и как визуализировать их в Tableau. Он еще сделал визуализацию «parametric parrot» (и другие визы) и написал пост про это.
Обычно под математической функцией мы представляем вид y=f(x), но это не единственная форма представления, можно представить функцию, например так: x=f(t) и y=f(t). Здесь t — это какой-то параметр.
Если увеличивать параметр t на каком-то интервале, то мы получим набор значений для x и y для параметра t. Вы можете сделать датасет, имеющий 101 строку, где t увеличивается от 0 до 1 with с шагом 0.01. Tableau это может визуализировать как диаграмму разброса, где будут показана 101 точка.
Параметрические уравнения для всех кривых моего виза с известными людьми были найдены ранее (я даже не знаю, кто их нашел) и сохранены в системе WolframAlpha. Там можно найти много других кривых, набирая в поиске: «person curves», «popular curves» или даже «marvel curves».
Можно перейти по следующим линкам, если хотите узнать как такие кривые можно получить в среде «Mathematica». Это описано в блоге Wolfram Research (1, 2, 3)
1. Разбираем функции «Person Curves»
Для примера можно выбрать любую кривую и работать с ней. «Person Curves» не имеет перевода на русский, это кривые, описывающие изображения людей. Я буду дальше в этой статье работать с кривой, описывающей портрет Илона Маска Elon Musk Curve. После того, как мы нашли подходящую кривую, можно посмотреть на preview кривой и на параметрические уравнения этой кривой.
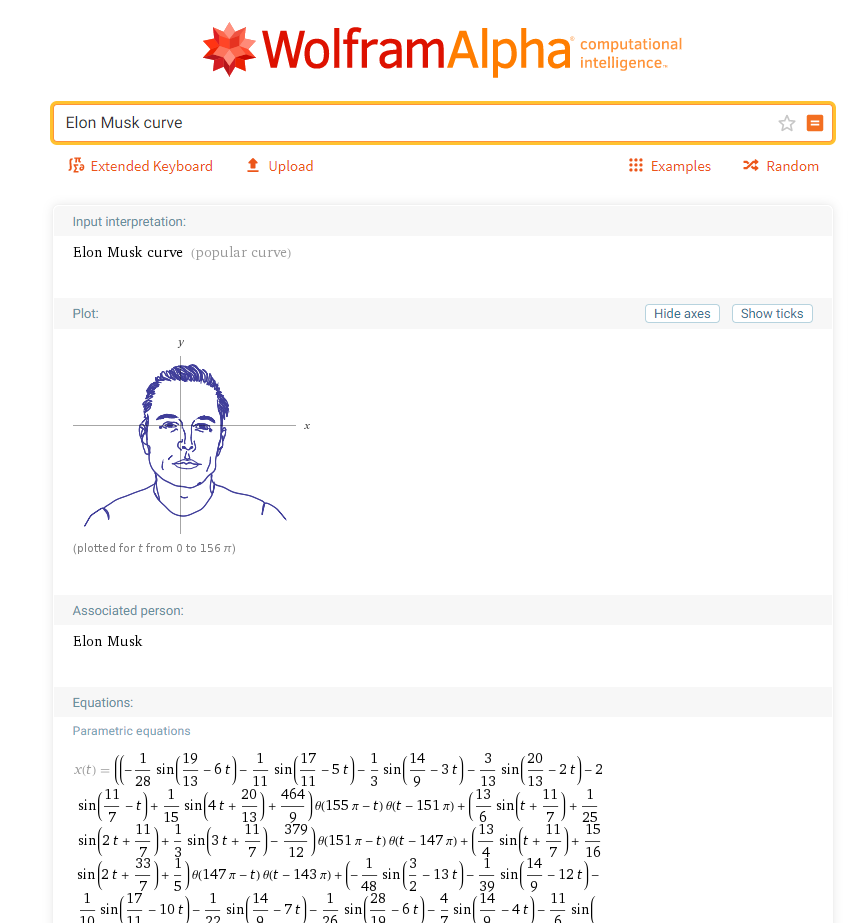
Далее нажмите plain text как на рисунке снизу:
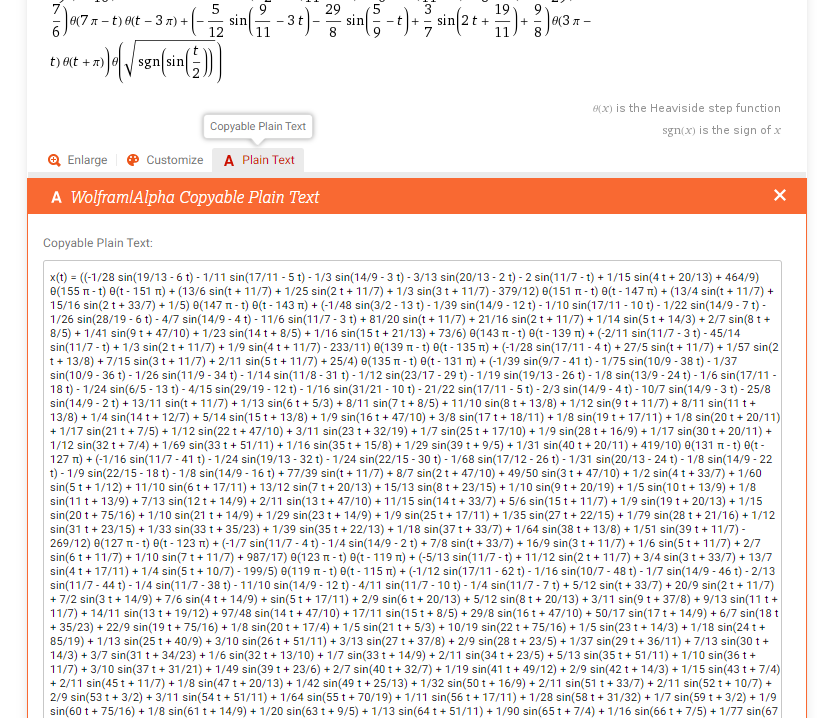
Этот текст — параметрические уравнения в текстовом формате, он содержит 2 строки 2 strings: одна строка для x(t), а другая для y(t). Этот текст нужно скопировать кликом по нему.
Следующие шаги будут включать работу с кодом Python 3. Вам нужен Python на рабочем компьютере, если хотите дальше работать с параметрическими уравнениями «Person Curves». Также будут примеры работы в PyCharm это integrated development environment (IDE) для Python.
Хорошо. Сейчас надо выяснить, какие функции содержат в себе параметрические уравнения Ok. Уравнения в текстовом виде очень большие (свыше 17000 символов в каждом), но их можно разбить на функции 3х типов (с произвольными коэффициентами):
1. 1/25 sin(12 t + 11/7)
2. θ (139 π – t)
3. θ(sqrt(sgn(sin(t/2))))
где θ (x) — ступенчатая функция Хевисайда, а sgn(x) — сигнум функция
Ниже показаны две этих единичных функции:
Ступенчатая функция Хевисайда
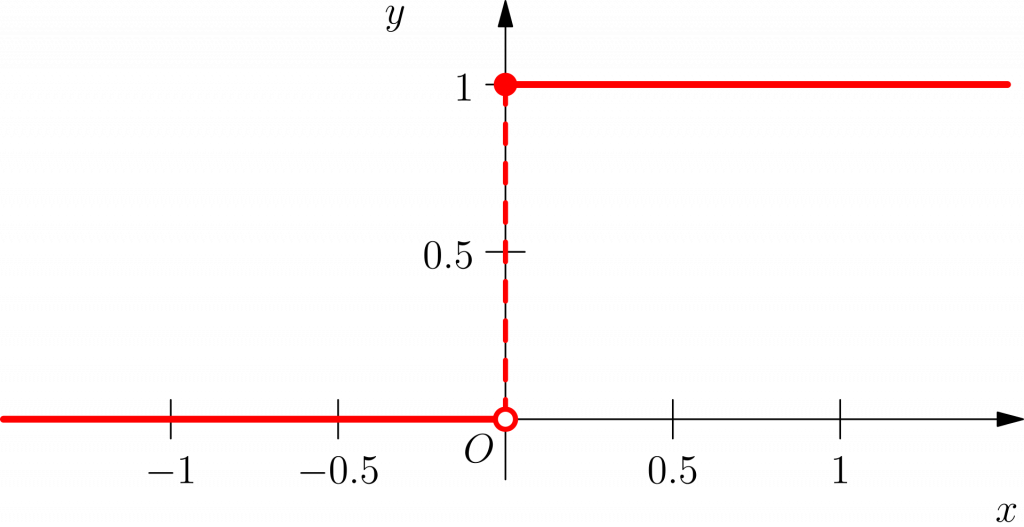
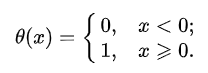
Сигнум
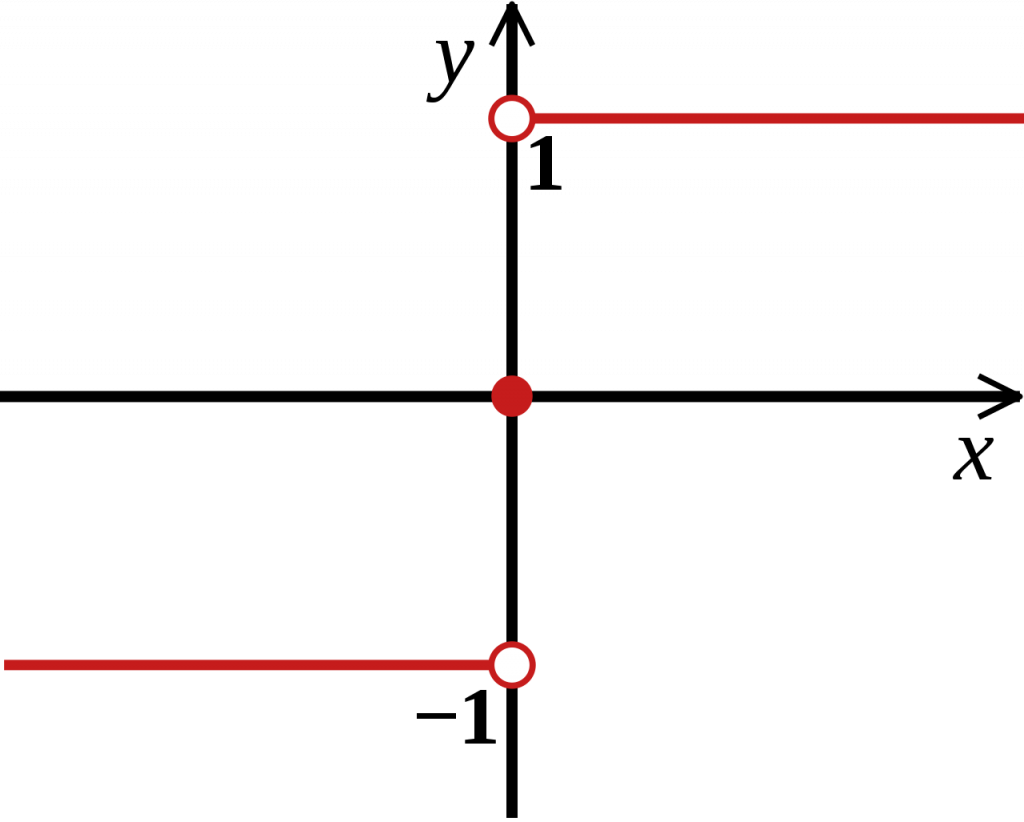
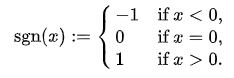
* изображения из википедии
2. Конвертирование параметрических уравнений в формат Tableau
Теперь нам нужно преобразовать функции в формат Tableau. Надо добавить знак умножения ‘*‘ signs и использовать IIF and IF/THEN в вычислениях для преобразования функци Хевисайда и сигнум в формат Tableau format. Ниже показаны те же функции в формате Tableau:
1. 1/25 *sin(12*[t] + 11/7)
2. *IIF(139*PI() –[t]<0,0,1)
3. *IIF((sqrt(IF sin([t]/2)<0 THEN -1 ELSEIF sin([t]/2)>0 THEN 1 ELSE 0 END))<0,0,1)
Теперь будем подставлять эти вычисления в исходные параметрические уравнения
Используем Python
Следующий питоновский код преобразует исходные уравнения в формат Tableau.
Ссылка на код и сам код:
'''
The code allows converting parametric equations from https://www.wolframalpha.com/
1. Find a person curve on the site
2. Click on 'plain text' below a snippet with equations and copy the text
3. Create an empty file 'Text.txt' on your local computer in a Python project folder where and paste the text. Close the file
4. Run the script on your computer
5. Open the 'Text.txt' file and copy the text
6. Open a new project in Tableau, create a calculation X and paste the text. There will be 2 strings pasted.
7. Cut a lower string ad click 'Ok'
8. Create a new calculation 'Y' and paste it, click 'Ok'
Now we have parametric equation for X and Y where t is a variable
'''
import re
import os
with open('Text.txt', encoding='utf-8', mode='r') as g:
old_data = g.read()
new_data = old_data.replace('θ', 'O')
with open ('Text.txt', encoding='utf-8', mode='w') as g:
g.write(new_data)
with open('Text.txt', encoding='utf-8', mode='r') as g:
old_data = g.read()
new_data = old_data.replace(' π', '*PI')
with open ('Text.txt', encoding='utf-8', mode='w') as g:
g.write(new_data)
replacements2 = {' t': '*t', ' sin': '*sin'}
with open('Text.txt') as infile, open('Text1.txt', 'w') as outfile:
for line in infile:
for src, target in replacements2.items():
line = line.replace(src, target)
outfile.write(line)
with open('Text1.txt', 'r') as x:
old_data = x.read()
new_data = re.sub('O\((.*?)\)', r'*IIF(\1<0,0,1)', old_data)
with open ('Text1.txt', 'w') as y:
y.write(new_data)
with open('Text1.txt', encoding='utf-8', mode='r') as g:
old_data = g.read()
new_data = old_data.replace('*PI', '*PI()')
with open ('Text1.txt', encoding='utf-8', mode='w') as g:
g.write(new_data)
replacements = {'-*t' :'-t', '+*t' :'+t', '-*sin' :'-sin', '+*sin' :'+sin', '+*PI()' :'+PI()' , '-*PI()' :'-PI()', 'x(t) =':'', 'y(t) =':'', '*IIF(sqrt(sgn(sin(t/2<0,0,1))))': '*IIF((sqrt(IF sin([t]/2)<0 THEN -1 ELSEIF sin([t]/2)>0 THEN 1 ELSE 0 END))<0,0,1)'}
with open('Text1.txt') as infile, open('Text.txt', 'w') as outfile:
for line in infile:
for src, target in replacements.items():
line = line.replace(src, target)
outfile.write(line)
os.remove('Text1.txt')Операции, которые выполняет этот код:
1. Замена греческих букв θ и π на 'O' и '*PI' соответственно, чтобы легче было работать дальше (большое спасибо Егору Ларину и Константину Брудар за помощь с UTF-8)
with open('Text.txt', encoding='utf-8', mode='r') as g:
old_data = g.read()
new_data = old_data.replace('θ', 'O')
with open ('Text.txt', encoding='utf-8', mode='w') as g:
g.write(new_data)
with open('Text.txt', encoding='utf-8', mode='r') as g:
old_data = g.read()
new_data = old_data.replace(' π', '*PI')
with open ('Text.txt', encoding='utf-8', mode='w') as g:
g.write(new_data)2. Вставка знака умножения '*' перед 't' и 'sin'
replacements2 = {' t': '*t', ' sin': '*sin'}
with open('Text.txt') as infile, open('Text1.txt', 'w') as outfile:
for line in infile:
for src, target in replacements2.items():
line = line.replace(src, target)
outfile.write(line)3. Преобразование функции Хевисайда в формат Tableau с помощью регулярных выражений.
with open('Text1.txt', 'r') as x:
old_data = x.read()
new_data = re.sub('O\((.*?)\)', r'*IIF(\1<0,0,1)', old_data)
with open ('Text1.txt', 'w') as y:
y.write(new_data)4. Замена '*PI' на функцию Tableau '*PI()'
with open('Text1.txt', encoding='utf-8', mode='r') as g:
old_data = g.read()
new_data = old_data.replace('*PI', '*PI()')
with open ('Text1.txt', encoding='utf-8', mode='w') as g:
g.write(new_data)5. Замены: '-*t' :'-t', '+*t' :'+t', '-*sin' :'-sin', '+*sin' :'+sin', '+*PI()' :'+PI()' , '-*PI()' :'-PI()' для случаев, когда нет коэффициентов перед t,sin и PI(). Замена выражения функции сигнум. Удаление 'x(t) =', 'y(t) =' – они не нужны.
replacements = {'-*t' :'-t', '+*t' :'+t', '-*sin' :'-sin', '+*sin' :'+sin', '+*PI()' :'+PI()' , '-*PI()' :'-PI()', 'x(t) =':'', 'y(t) =':'', '*IIF(sqrt(sgn(sin(t/2<0,0,1))))': '*IIF((sqrt(IF sin([t]/2)<0 THEN -1 ELSEIF sin([t]/2)>0 THEN 1 ELSE 0 END))<0,0,1)'}
with open('Text1.txt') as infile, open('Text.txt', 'w') as outfile:
for line in infile:
for src, target in replacements.items():
line = line.replace(src, target)
outfile.write(line)6. Удаление временного файла ‘Text1.txt’.
os.remove('Text1.txt')Скрипт можно оптимизировать, но разбиение на несколько шагов позволяет проще его понять.
Запустим PyCharm и создадим новый проект, создадим в проекте файл ‘Text.txt’ с параметрическими уравнениями и файл .py (test.py в нашем случае). Будем дальше работать с этими файлами.
Скопируем весь код, приведенный выше, и вставим его в PyCharm.
Запустим код.
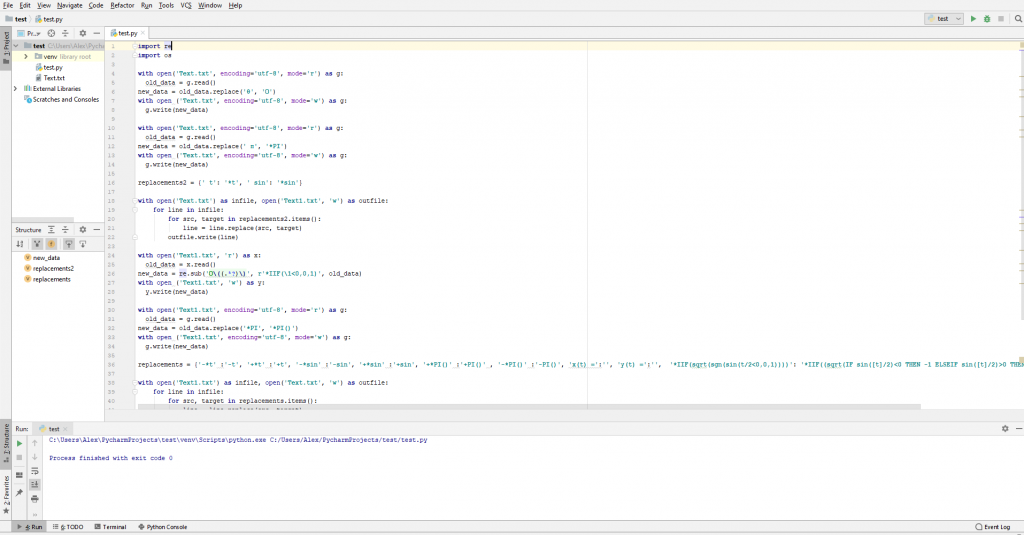
После успешного выполнения кода и надписи ‘Process finished with exit code 0’, откроем ‘Text.txt’ и скопируем все оттуда.
Сделаем датасет в MS Excel c одним столбцом ‘Num’ и двумя значениями в столбце:
Num
0
500
3. Рисование функциями в Tableau
Запустим Tableau Desktop и подключим на Excel файл как источник данных.
Создадим новое вычисление ‘X’ и вставим весь результат работы кода на питоне, который мы скопировали из файла ‘Text.txt’ .

Получим 2 строки (верхняя строка для X а нижняя - для Y), вырежем нижнюю строки и нажмем ‘Ok’. Получили вычисление X.
Создаем новое вычисление Y и вставляем туда строку для Y. Нажимаем ‘Ok’. Теперь у нас есть вычисление Y.
Создаем bin (ttt в моем случае)
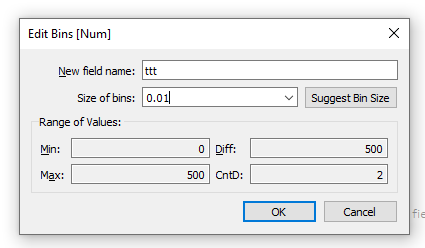
Создаем вычисление с INDEX() . Параметр Step в вычислении можно будет переключать, об этом поговорим дальше. На самом деле вместо параметра можно поставить 100 или другое число. Чем больше знаменатель, тем меньше шаг будет между соседними точками значения t , следовательно, более сложной получится кривая и более детализированной будет картинка.
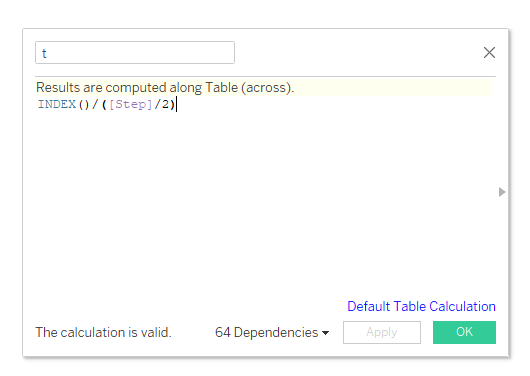
Перетащите вычисления X, Y и ttt на лист Tableau как на скриншоте снизу. X и Y - это табличные вычисления. Выберите 'compute using' - ttt для обоих вычислений. Теперь можно любоваться на портрет.
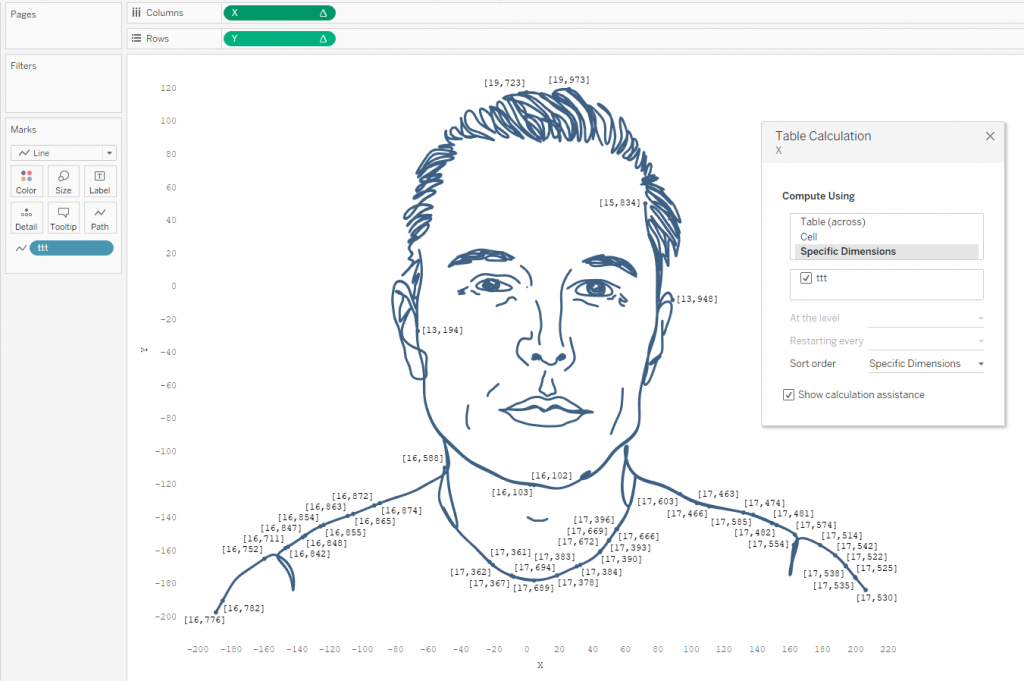
Note. На сайте WolframAlpha site ниже кривой the Elon Musk curve написано 'plotted for t from 0 to 156π'. Это означает, что X и Y = 0 за пределами этого интервала. Когда t>156π X и Y =0 можно увидеть точку в начале координат.
В Tableau возможно фильтровать эти точки в начале координат, но это снизит производительность. Также можно размер bin подогнать под этот интервал. Для этого случая размер такой: 0.0172, при этом мы строим функцию на интервале от 0 до 156π.
Настройки формы кривых
Для большей интерактивности я сделал 2 параметра:
- Complexity Step
- Drawing Step
The step of complexity (шаг сложности) я уже упоминал выше как часть вычисления t. Этот шаг меняет интервал между соседними точками кривой. Ниже приведены кривые для разных значений этого шага:



Можно видеть из этих картинок что увеличение шага сложности уменьшает значение t, следовательно будет увеличиваться число точек на интервале (0 ; 156π)
The Drawing Step (шаг рисования) определяет порядок отрисовки точек.

Complexity Step = 100

Complexity Step = 100
Чтобы сделать имитацию рисования от руки, я сделал вычисление, отбрасывающее все шаги рисования выше определенного значения параметра Drawing Step. То есть, увеличивая этот параметр, портрет будет рисоваться постепенно.
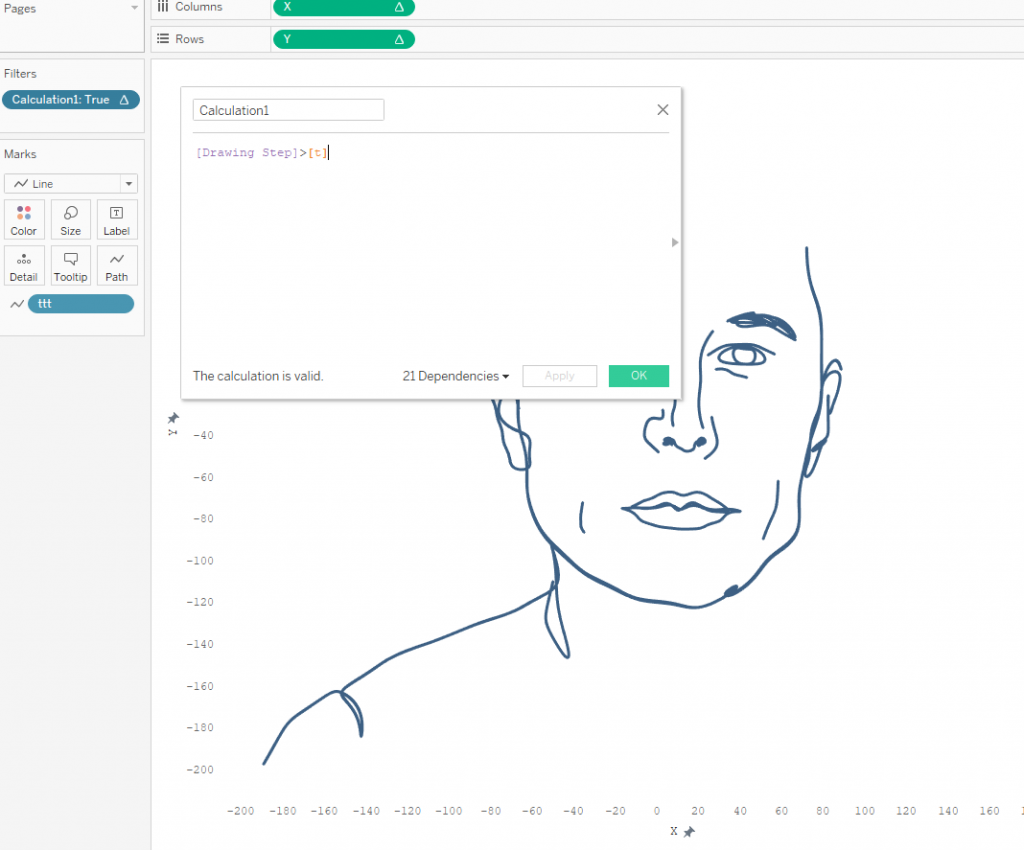
И финальный результат:

Рисуя портреты с различными значениями параметров кривых, можно получать очень интересные вещи:

P.S. При подготовке статье я нашел в блоге Ken Flerlage следующее:

Это еще раз доказывает, что у табло практически нет границ для визуализации данных.
Заключение
Параметрические портреты в табло - это очень необычный тип визуализаций. Но сама идея того, что можно нарисовать что угодно при помощи математических функций очень вдохновляет. Быть может, нашу вселенную можно описать одной функцией The universe works on a math equation (спасибо Adam Mico за эту песню)?
