Транспортная задача или задача Монжа-Канторовича — это задача линейного программирования об оптимальном плане перевозок грузов из пунктов отправления в пункты потребления, с минимальными затратами на перевозки. В классической задаче рассматривается план перевозок однородного продукта из однородных пунктов наличия в однородные пункты потребления на однородных транспортных средствах. Решение транспортных задач имеет огромную роль в экономике, и исследования в направлении решений таких задач принесли успехи еще во времена СССP. Большую роль в исследовании решений таких задач сыграл наш соотечественник, лауреат Нобелевской премии по экономике, Леонид Канторович. Возможно, определения выше звучат сложно, поэтому в этой статье я попробую на примерах простым языком объяснить как решаются транспортные задачи в Python и Tableau, и как можно визуализировать результаты решений.
1. Постановка задачи
На острове Манхеттен в Нью-Йорке есть 392 отеля, из каждого отеля выселяется один постоялец, за каждым из которых нужно отправить такси, чтобы доставить всех в аэропорт. Постояльцы выселяются одно время, 392 такси разбросаны по Манхеттену. Нужно отправить каждую машину к одному отелю так, чтобы все маршруты были оптимальными, то есть, в сумма всех расстояний была минимальной. Для упрощения задачи не будем учитывать геометрию улиц, а просто найдем расстояния между отелями и текущими положениями такси. Данные об отелях штата New York я нашел на kaggle, выбрал оттуда 392 отеля так чтобы получалась компактная картинка на карте. Выборку данных на карте делал в Tableau — так сразу видны точки, и можно быстро убрать лишние либо с помощью фильтров, либо используя Exclude прямо на карте. Получилась такая картинка:
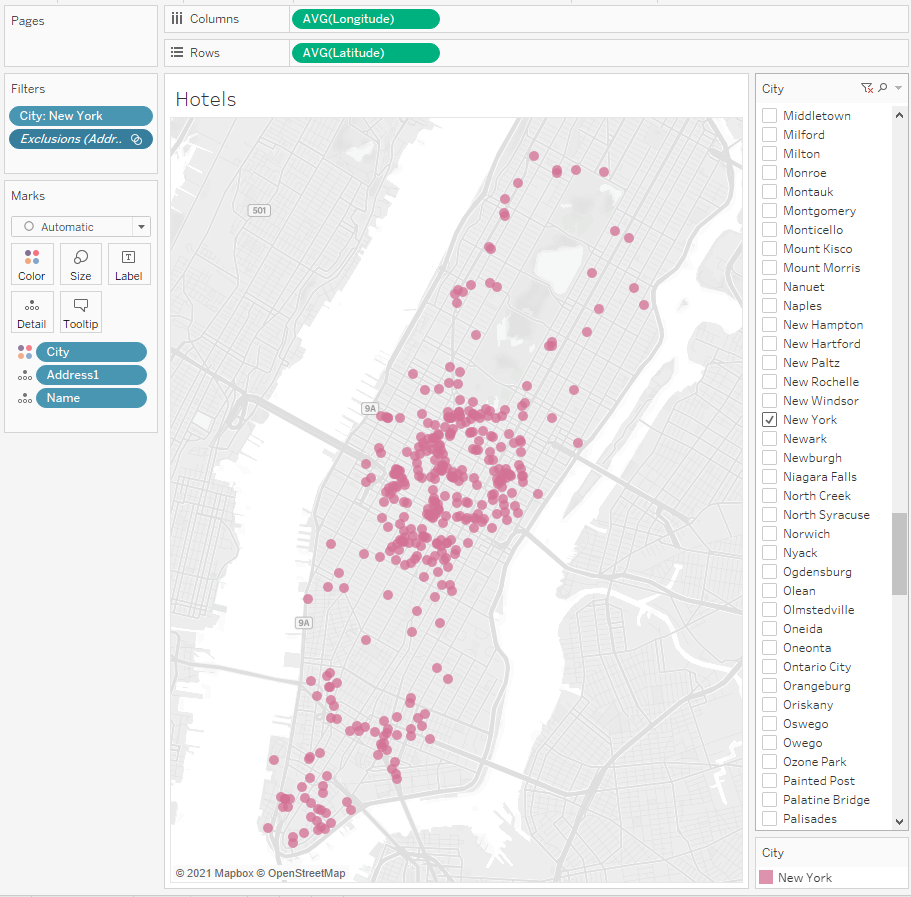
Все эти точки с координатами, названиями и адресами отелей выгрузил в файл Hotels.csv
Теперь нам нужно как-то раскидать такси по Манхэттену. В сети много датасетов по ДТП, и по Нью-Йорку такие датасеты обычно корректны. На kaggle есть датасет за 2016 год. ДТП происходили на улицах Манхэттена, поэтому можно взять 392 локации и считать их местами нахождения такси. Я подключил этот датасет к Tableau и фильтрами оставил 392 места старта такси так, чтобы эти локации находились примерно на той же части острова что и отели:
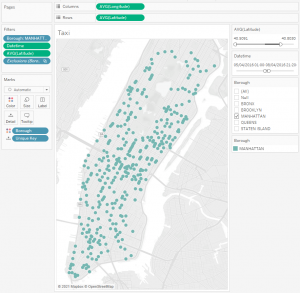
Эти точки с координатами выгрузил в файл Taxi.csv
Сейчас мы видим точки старта (такси) и точки финиша (отели). Дальше будем искать оптимальный набор маршрутов, то есть, решать транспортную задачу.
2. Поиск оптимального набора маршрутов
Задачу будем решать в Python. Будем использовать библиотеку POT: Python Optimal Transport.
В документации библиотеки есть пример задачи оптимального транспорта между двумя наборами точек. Этот пример нам подойдет для понимания того как работает библиотека.
Код из примера я взял за основу, добавил чтение координат из файлов Hotels.csv и Taxi.csv, а также выгрузку матрицы перехода:
import numpy as np
import pandas as pd
import csv
import matplotlib.pylab as pl
import ot.plot
n = 392 # nb samples
data1 = pd.read_csv ('C:/Docs/Tableau/Projects/Optimal Transport/New York Taxi/Final/Taxi.csv', encoding="ISO-8859-1", nrows=n)
data2 = pd.read_csv ('C:/Docs/Tableau/Projects/Optimal Transport/New York Taxi/Final/Hotels.csv', encoding="ISO-8859-1", nrows=n)
a1 =pd.DataFrame (data1, columns=["Longitude", "Latitude"])
a2 =pd.DataFrame (data2, columns=["Longitude", "Latitude"])
xs = np.array(a1)
xt = np.array(a2)
print(a1)
print(a2)
a, b = np.ones((n,)) / n, np.ones((n,)) / n # uniform distribution on samples
# loss matrix
M = ot.dist(xs, xt)
M /= M.max()
pl.figure(1)
pl.plot(xs[:, 0], xs[:, 1], '+b', label='Source samples')
pl.plot(xt[:, 0], xt[:, 1], 'xr', label='Target samples')
pl.legend(loc=0)
pl.title('Source and target distributions')
pl.figure(2)
pl.imshow(M, interpolation='nearest')
pl.title('Cost matrix M')
G0 = ot.emd(a, b, M)
pl.figure(3)
pl.imshow(G0, interpolation='nearest')
pl.title('OT matrix G0')
pl.figure(4)
ot.plot.plot2D_samples_mat(xs, xt, G0, c=[.5, .5, 1])
pl.plot(xs[:, 0], xs[:, 1], '+b', label='Source samples')
pl.plot(xt[:, 0], xt[:, 1], 'xr', label='Target samples')
pl.legend(loc=0)
pl.title('OT matrix with samples')
table=[]table2=[]i = 0
j = 0
while j < n:
while i < n:
if G0[i,j]>0:
table.append([i,j])
i = i + 1
table2.append(table)
i = 0
j = j + 1
print(type(table2))
pl.show()
with open('C:/Docs/Tableau/Projects/Optimal Transport/New York Taxi/Final/transition_matrix.csv', "w", newline="") as f:
writer = csv.writer(f)
writer.writerows(table)
Давайте разберемся как работает код.
n = 392 — это количество строк, которые читаем из файлов Hotels.csv и Taxi.csv. Строки записываем в массивы xs, и xt соответственно, отображаем точки массивов на диаграмме разброса. Получаем точки старта (Source samples, точки такси) и точки финиша (Target samples, точки отелей):
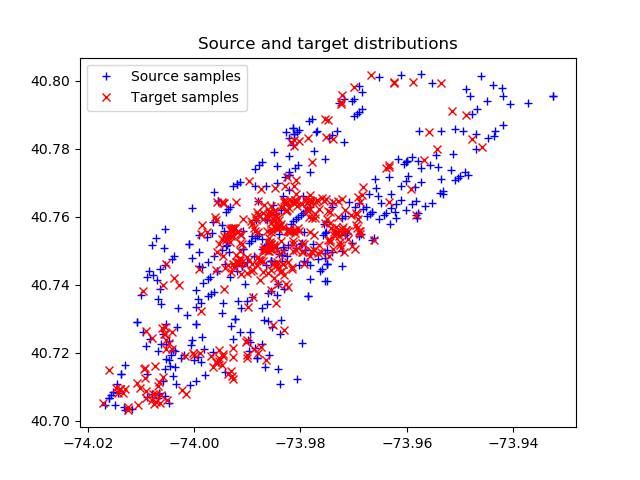
Далее начинается самое интересное — вычисляются все расстояния между группами Source и Target и строится матрица расстояний (затрат на перемещение), в которой цвет кодирует расстояние между точками с Source id и Target id:
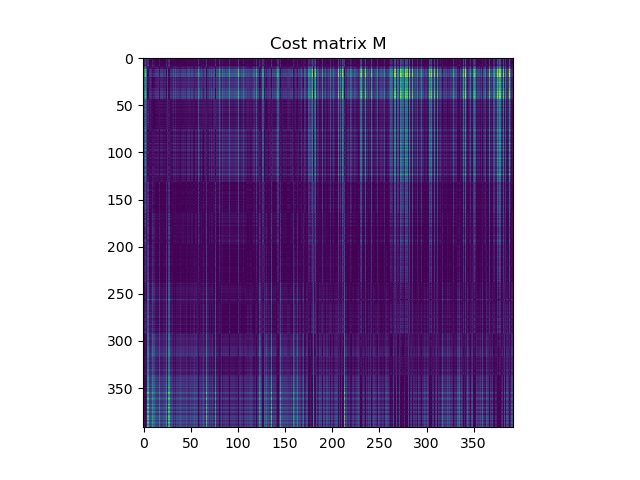
Чем светлее точка, тем меньше расстояние между точками.
После этого на основании матрицы расстояний строится матрица оптимального транспорта. В ней одной точке из группы Source ставится в соответствие одна точка группы Target. Все светлые точки на матрице ниже показывают такие соответствия:
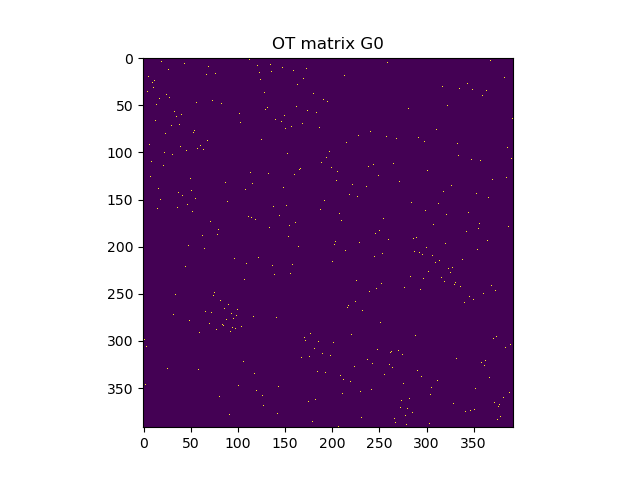
На следующем рисунке визуализируются найденные соответствия точек, то есть, показываются оптимальные расстояния между Source и Target.
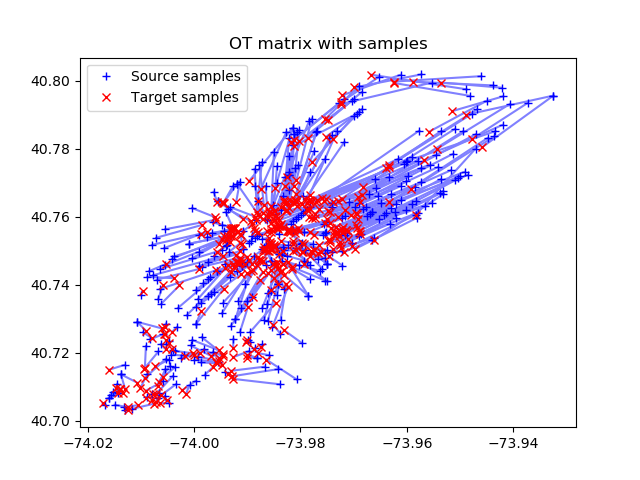
Последняя картинка — это ровно то, что мы хотели найти — оптимальный набор маршрутов такси до отелей.
В конце код записывает соответствия Source id — Target id в файл .csv в виде двух столбцов, и мы получаем файл ‘transition_matrix.csv‘, который поможет соединить источники Hotels.csv и Taxi.csv по оптимальным id.
Файл ‘transition_matrix.csv‘ выглядит так:
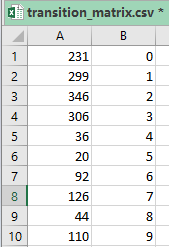
Здесь первый столбец — это id локаций файла Taxi.csv, а второй столбец — id отелей в Hotels.csv.
Эти столбцы добавим в файлы. Например, для Taxi.csv это будет выглядеть так:

Аналогично сделаем в файле Hotels.csv.
Важно: В этом примере для простоты мы работаем с декартовой системой координат и не учитываем изменение долготы. Один градус долготы соответствует 111км на экваторе, а по мере движения к полюсам это расстояние уменьшается, и при расчетах расстояний на картах это надо учитывать.
3. Визуализация маршрутов в Tableau
Подключим оба файла к Tableau и сделаем UNION:
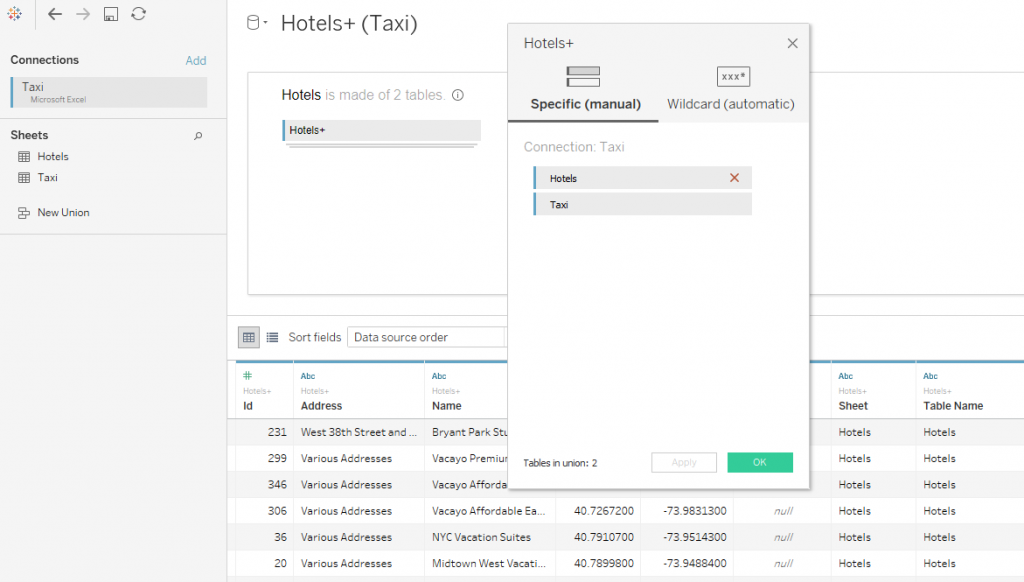
В визуализации можно:
- Использовать анимацию и показать анимированные переходы между начальными и конечными точками
- Построить маршруты, cоединив точки линиями
Давайте сначала нарисуем маршруты такси. Такси стартуют с красных точек и движутся к голубым:
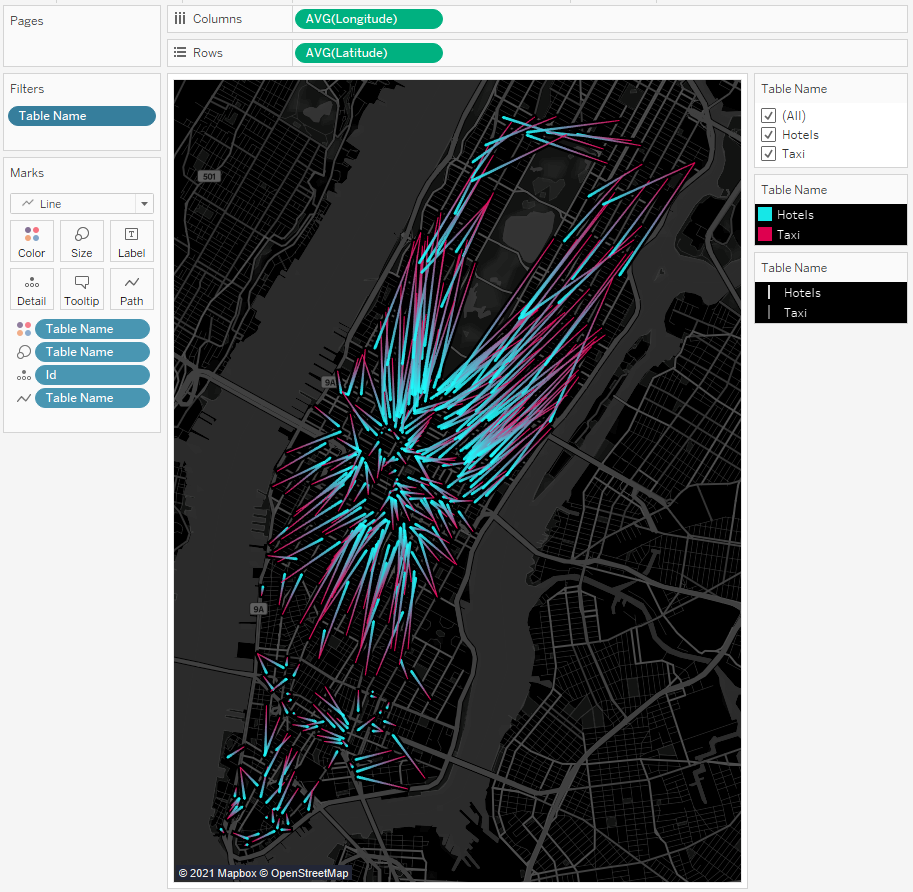
Используя фильтр Table Name можно включать и отключать локации такси или точки отелей:
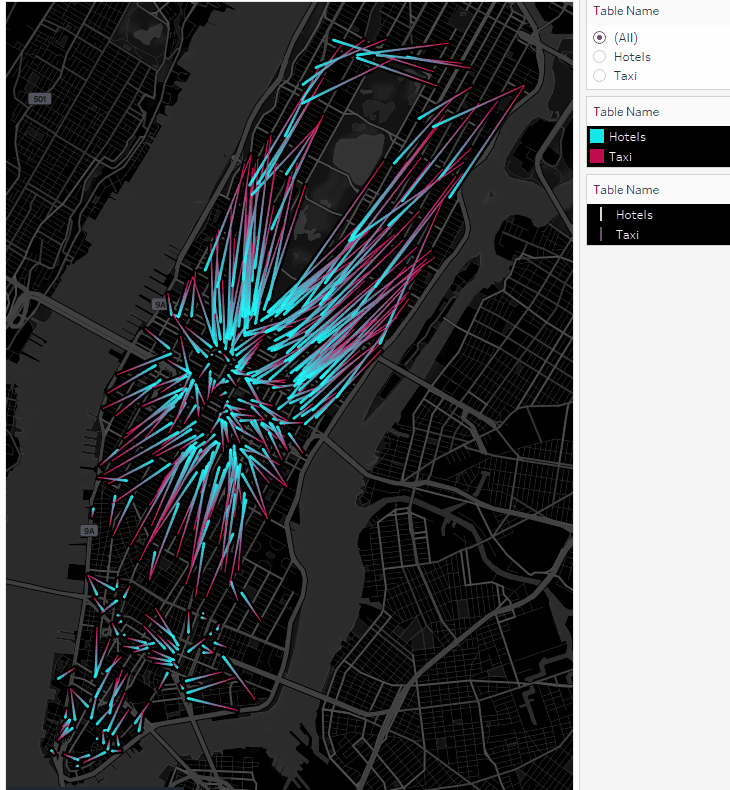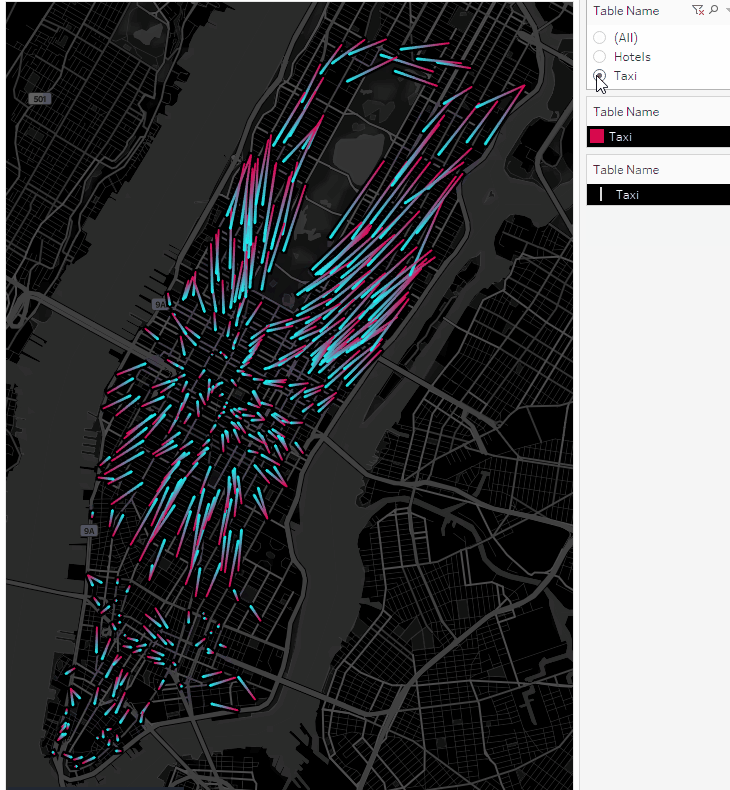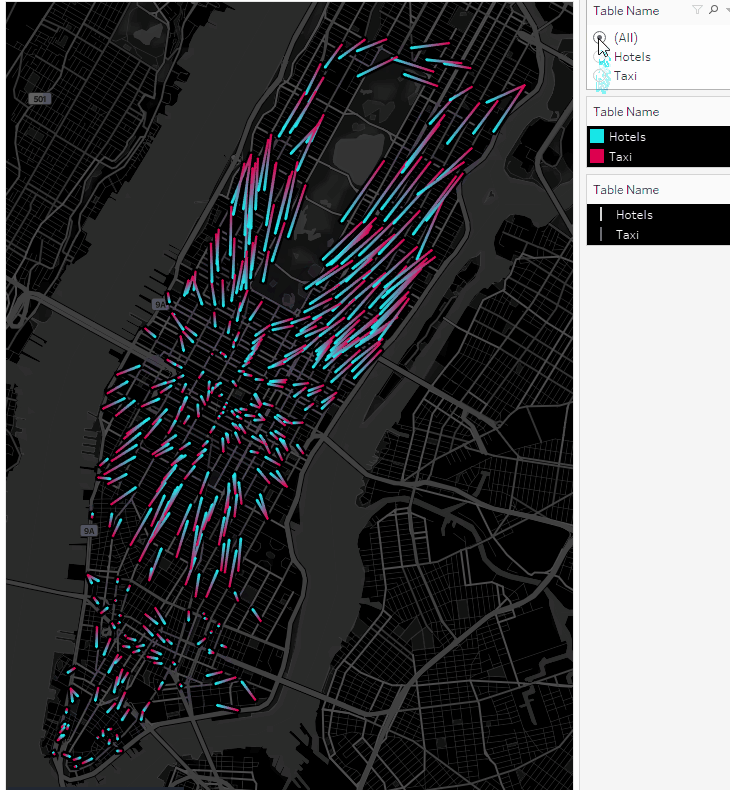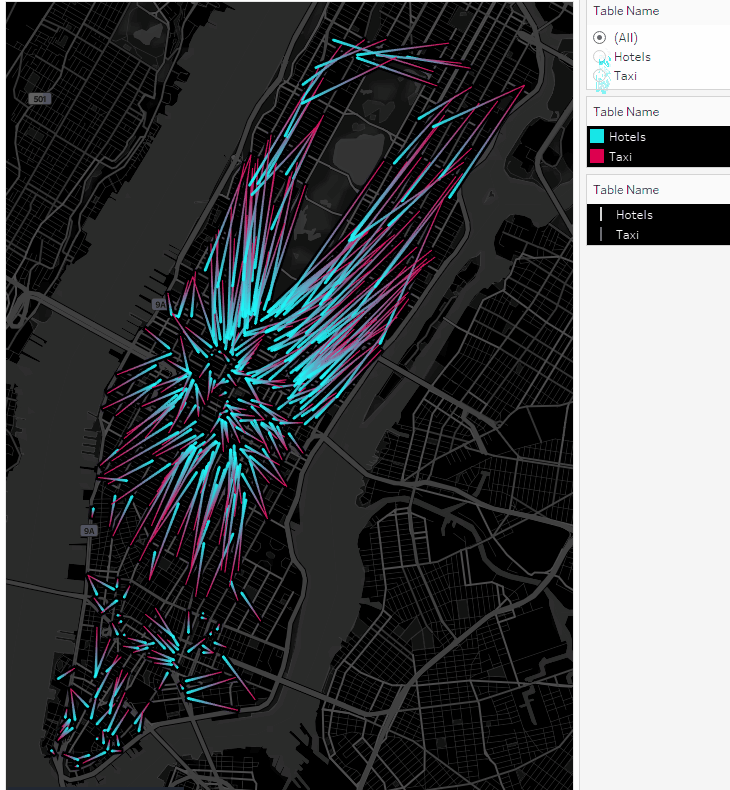
Получили анимированные маршруты. Теперь давайте построим перемещения такси в виде точек на карте.
Для этого создадим новый источник и сджойним два .csv файла по id:
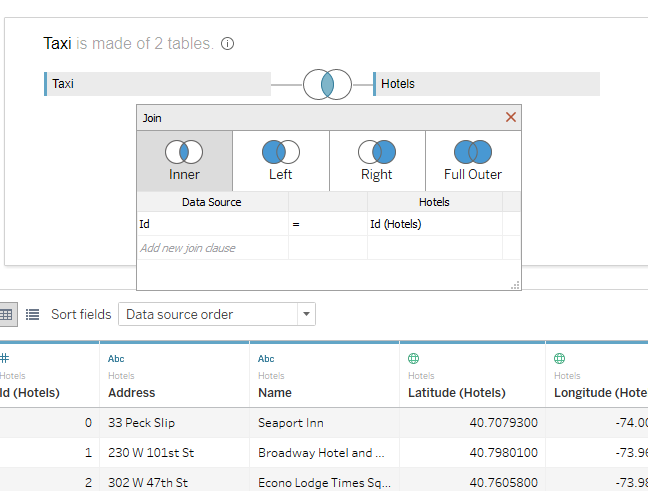
Создадим числовой параметр Parameter 1 со значениями 1 и 2, а также два вычисления Lat и Long:
IF [Parameter 1]=1 THEN [Latitude (Taxi)] ELSE [Latitude (Hotels)] END
IF [Parameter 1]=1 THEN [Longitude (Taxi)] ELSE [Longitude (Hotels)] END
Этот параметр позволит переключать координаты такси на координаты отелей, и при включенной анимации увидим следующее:
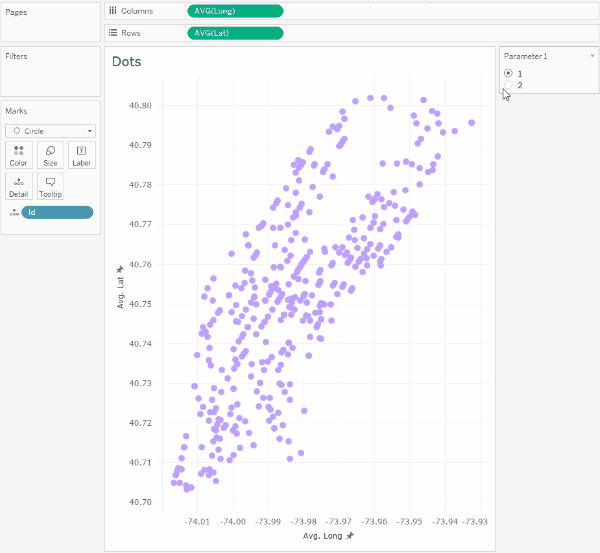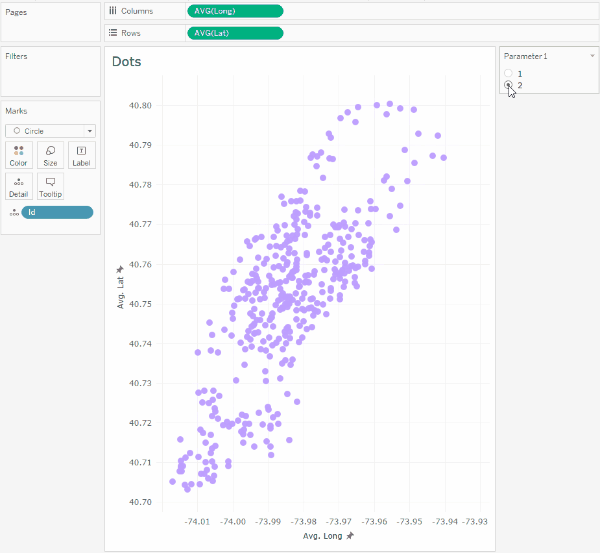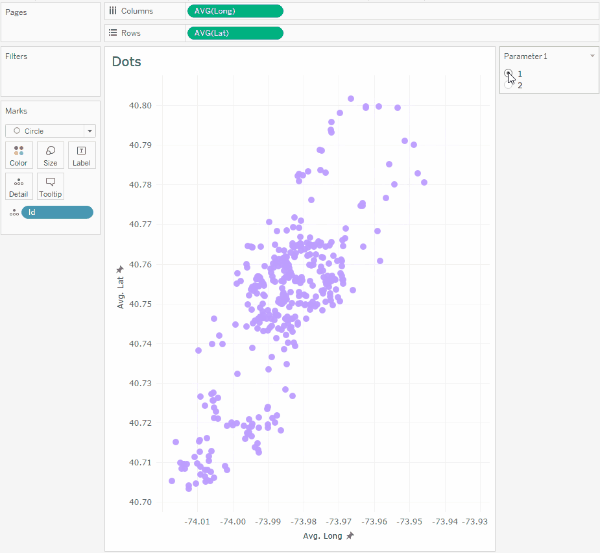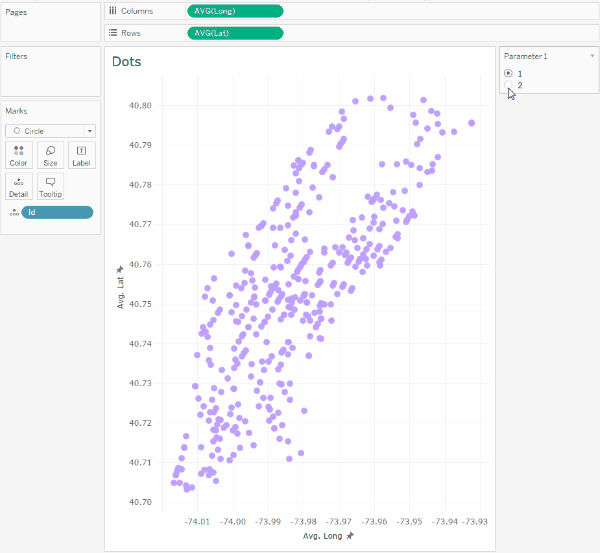
Надо заметить что на карте такие переходы в Tableau не анимируются, поэтому не будем присваивать полям Lat и Long географические типы широты и долготы.
Если на одном дашборде совместить лист с линиями маршрутов на карте и лист с точками, предварительно убрав заливку фона, сетку и оси координат, то получим следующую картинку, на которой один Tiled слой с картой переключается фильтром Table Name, а анимация точек на листе Floating переключается параметром.
 Таким образом, мы показали анимированные маршруты такси линиями, а сами такси — точками. На этом задачу поиска оптимальных маршрутов и их визуализации можно считать завершенной.
Таким образом, мы показали анимированные маршруты такси линиями, а сами такси — точками. На этом задачу поиска оптимальных маршрутов и их визуализации можно считать завершенной.
4. Неоптимальные маршруты
Ранее мы рассмотрели только оптимальные маршруты такси, при которых суммарная дистанция между машинами о отелями была бы минимальной. Однако интересно посмотреть насколько оптимальная картина отличается от самой неоптимальной.
Для этого надо преобразовать матрицу расстояний так чтобы минимальные цифры стали минимальными и наоборот. Можно добавить в код после строки M /= M.max() строку:
M = - M
В итоге матрица расстояний будет выглядеть так:
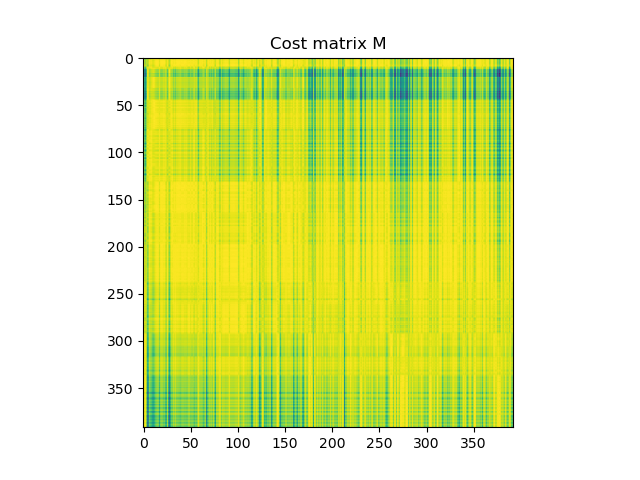
А маршруты перестроятся следующим образом:
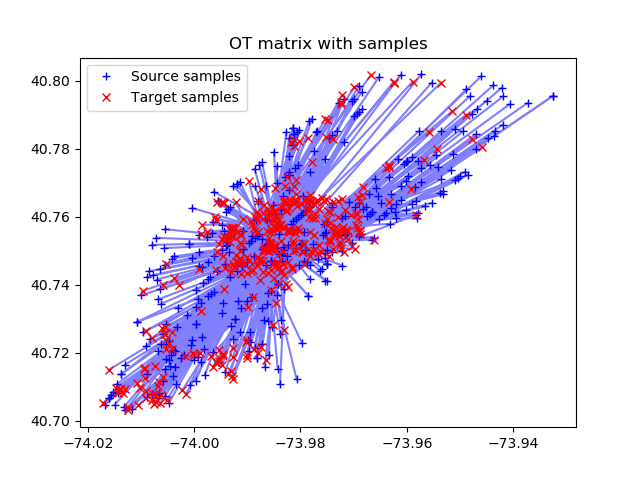
Можно сравнить оптимальные и неоптимальные маршруты. Нужно только добавить в датасет id для неоптимальных маршрутов, то есть, сделав джойн с еще одним датасетом Hotels, но уже с другими id.
Разница между оптимальной и неоптимальной картиной будет такой:
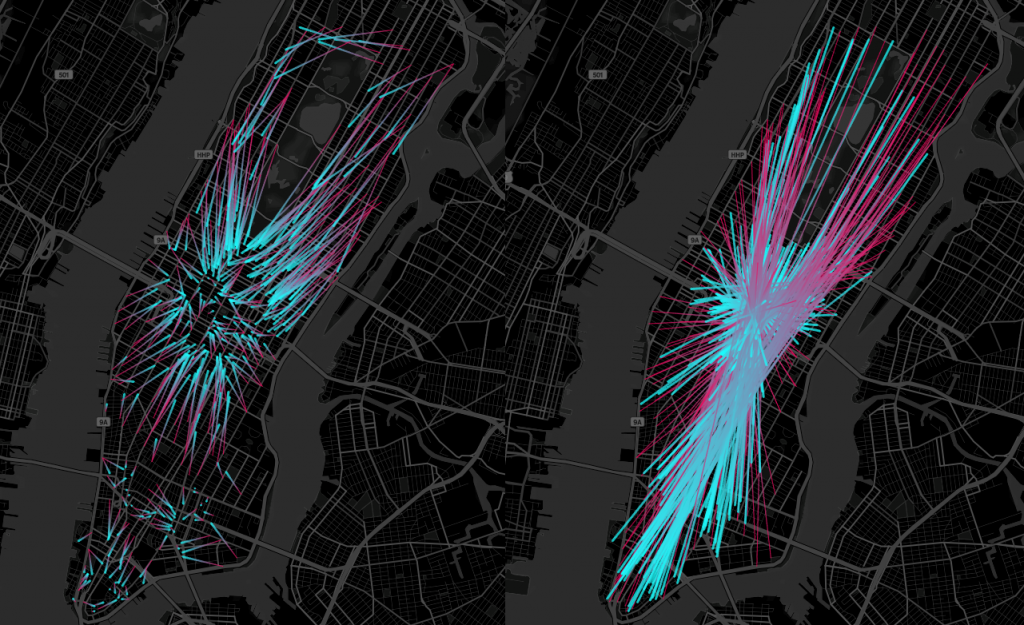
Для вычисления общих расстояний всех маршрутов используем формулу геометрического расстояния между двумя точками:
IF [Non Optimal]=TRUE THEN
SQRT(([Latitude (Hotels)]—[Latitude])^2 + ([Longitude (Hotels)]—[Longitude])^2)
ELSE
SQRT(([Latitude (Hotels NonOptimal)]—[Latitude])^2 + ([Longitude (Hotels NonOptimal)]—[Longitude])^2)
END
Чтобы перевести расстояния в мили, можно модифицировать формулу Distance:
IF [Non Optimal]=true THEN
69*SQRT(([Latitude (Hotels)]—[Latitude])^2 +
([Longitude (Hotels)]*COS(RADIANS([Longitude (Hotels)]))-
[Longitude]*COS(RADIANS([Longitude])))^2)
ELSE
69*SQRT(([Latitude (Hotels NonOptimal)]—[Latitude])^2 +
([Longitude (Hotels NonOptimal)]*COS(RADIANS([Longitude (Hotels NonOptimal)]))-
[Longitude]*COS(RADIANS([Longitude])))^2)
END
69 миль в одном градусе — именно это означает цифра 69. Если нужны километры, то 69 надо заменить на 111. Косинус угла долготы, на который умножается долгота компенсирует сближение меридианов к полюсам.
На картинке ниже видно что суммарные расстояние оптимальных и неоптимальных маршрутов отличается в 5 раз:

Финальная визуализация:

Этим мы показали, что при помощи метода Optimal Transport можно значительно сократить затраты на перемещение.
5. Применение Optimal Transport в анимации Tableau
Нативная анимация в Tableau существует уже больше года, и есть примеры анимированных переходов точек. Например, Extreme Weather Impacts on Health and Wellbeing Гэри Коллинза, Disney movies total gross 1937-2016 от yanming.guo, Titanic — Great loss of life автора Simon Rowe, моя визуализация о составе палаты представителей США.
О том как создавать подобные визуализации я писал в статье Точечные изображения на основе данных в Tableau.
Переходы одного изображения в другое обычно не учитывают длины траекторий между точками перехода — просто берутся порядковые номера строк в датасете и нумеруются по порядку. Но можно использовать Optimal Transport для расчета минимальных длин переходов.
Я сделал это в визуализации «Valentine’s Day«, где каждая точка — это один профиль Tableau Public:
Здесь для расчета переходов использовался точно такой же скрипт на Python, который приведен выше. Для двух соседних картинок были рассчитаны id точек:
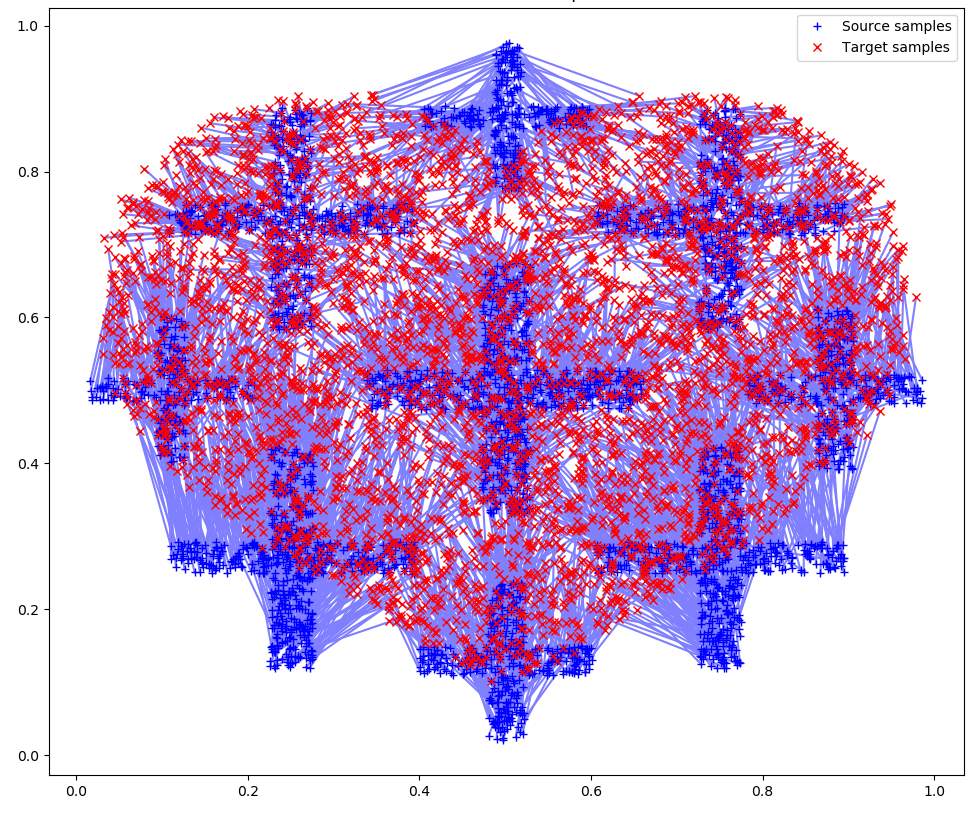
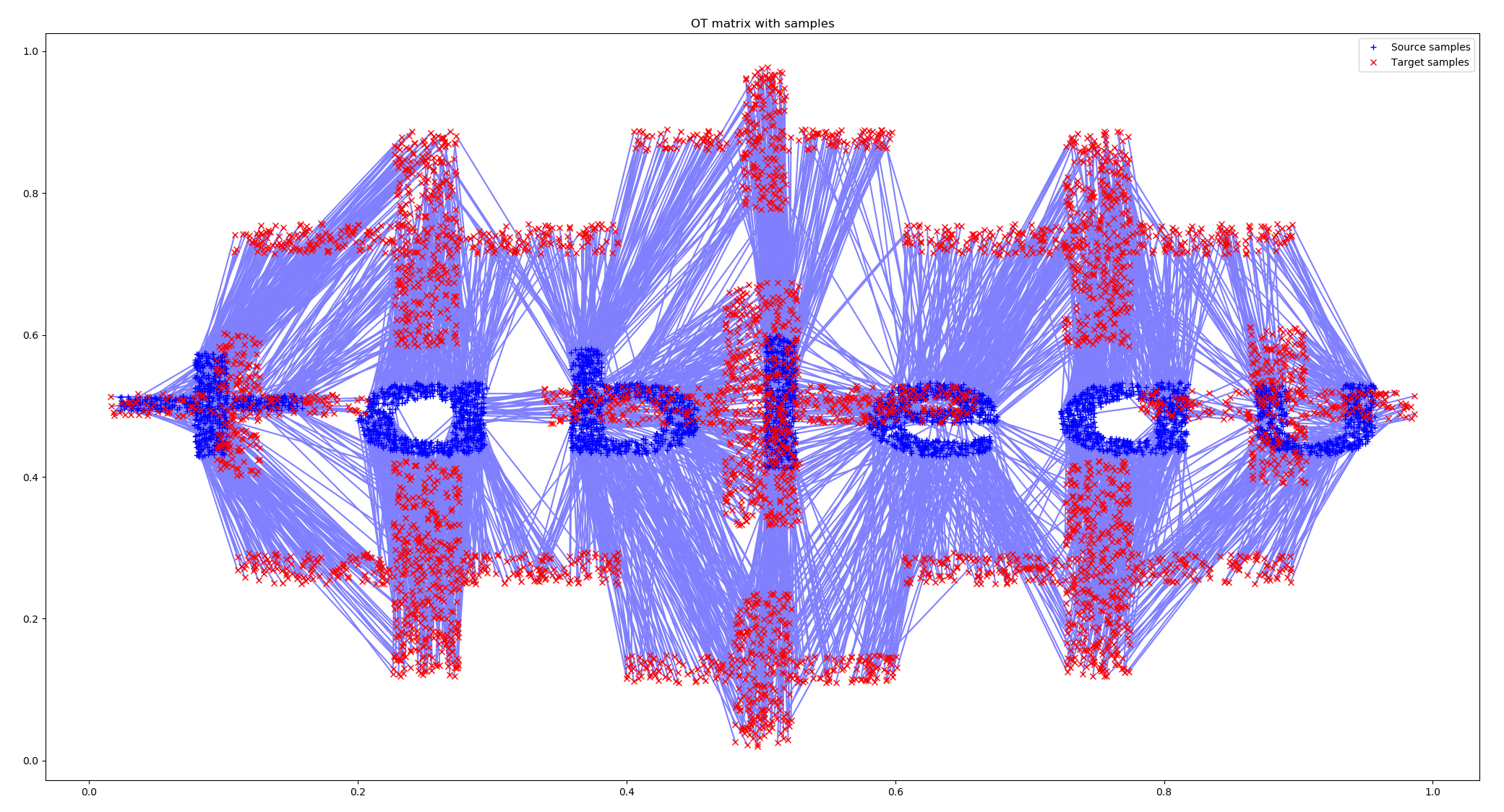
Такая анимация смотрится элегантнее, и создается эффект морфинга, а не просто хаотичных переходов одних точек в другие. Мне кажется, применение optimal transport в анимации может дать интересные визуализации.
Внимание: при увеличении количества точек в вашем датасете сильно увеличивается размер матрицы затрат. Например, при количестве точек 4500 в визуализации Valentine’s Day эта матрица имеет размер 4500×4500=20250000. При значительном увеличении точек скрипт не сможет их обработать — не хватит оперативной памяти
Заключение
Метод Optimal Transport можно применять как для бизнес-задач, в системах управления транспортом логистике, рассчитывая минимальные дистанции, а, следовательно, снижая время на перемещение, затраты на энергию, топливо и т.д. Также этот метод применяется для обработки изображений. Кроме этого, этот метод можно применять в анимации, создавая принципиально другие картины переходов между точками.

