Линейная регрессия в Tableau, часть 1. Временные ряды

Модель линейной регрессии используется для описания зависимости некоторой зависимой переменной Y от переменной X. Часто такие модели применяются для описания трендов величин. Тренды — это тенденции изменения величин в математике, они могут быть описаны линейными, логарифмическими, степенными и другими уравнениями. Кроме этого, трендами также называют графики, показывающие изменение некоторой величины во времени. В статье будет рассмотрены линейные тренды и линейная регрессия в Tableau.

В бизнес-среде графики величин, изменяющихся во времени очень популярны, в них можно найти много интересных инсайтов. Рассмотрим график курса евро к доллару по времени:

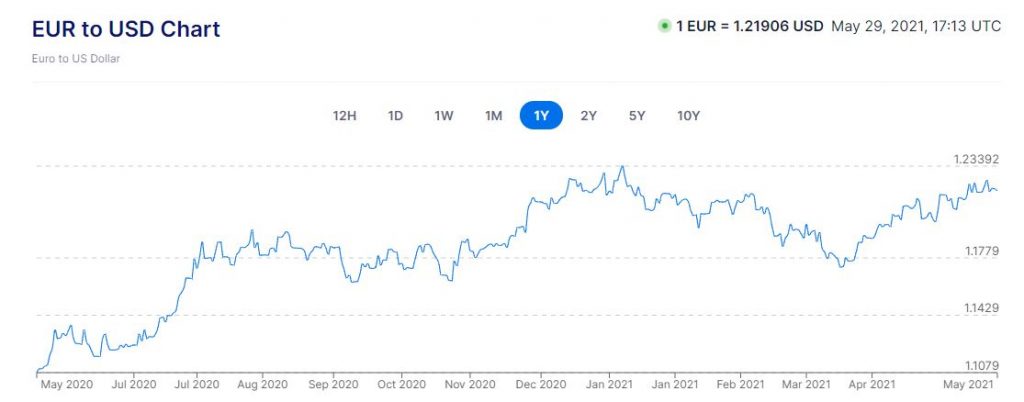
На графике показано изменение курса евро к доллару за каждый день на протяжении года. Мы видим, что на всем диапазоне данных курс рос, а на локальных диапазонах видны падения курса, то есть, курс евро изменялся волнами. По оси абсцисс здесь независимая переменная — время, а по оси ординат — зависимая функция курса евро.

Для того, чтобы количественно оценить тенденцию изменения курса евро, рассмотрим один из методов регрессионного анализа — нахождение линейной функции, описывающей тенденцию изменения курса евро к доллару за последние полтора года.

1. Линии тренда в Tableau

В Tableau есть возможность построения такого тренда нативно, для этого на панели Analysis надо найти Trend Line — Linear и перенести это на лист:

Возьмем данные по курсу EUR/USD за последние полтора года из источника. Построим график курса, а также линейный тренд:

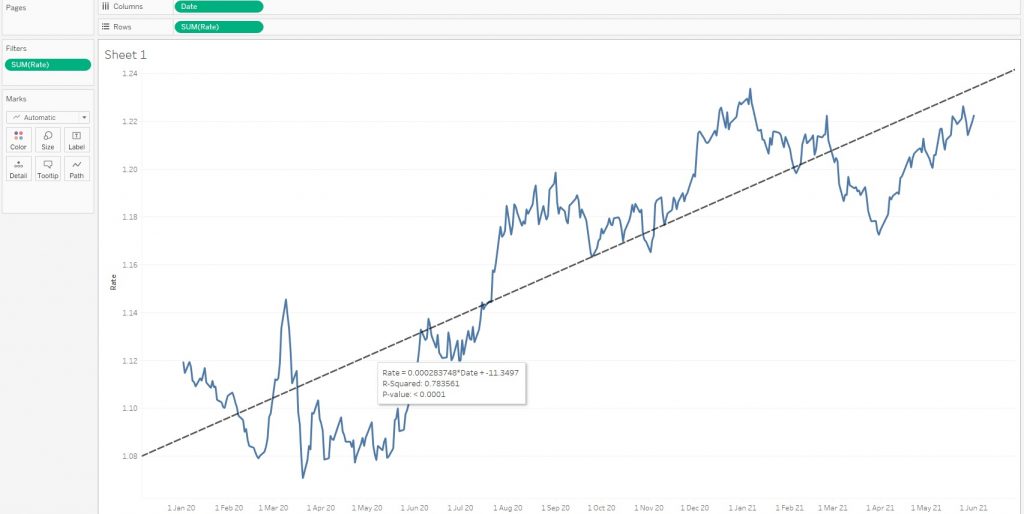
Это делается в Tableau буквально за пару кликов. При наведении на линию тренда можно увидеть следующую информацию:

Rate = 0.000283748 * Date + -11.3497
R-Squared: 0.783561
P-value: < 0.0001

Далее мы рассмотрим что обозначают первые две строки, и как эти цифры рассчитываются.

2. Метод наименьших квадратов

Выражение Rate = 0.000283748 * Date + -11.3497 описывает уравнение прямой вида y = ax + b. Эта прямая описывает линейный тренд и она показана на графике выше пунктирной линией.

Давайте найдем коэффициенты a и b при помощи вычислений в Tableau. Метод наименьших квадратов основан на минимизации суммы квадратов отклонений функций от искомых переменных. Иными словами нам нужно найти функцию кривой в общем виде (или функцию прямой в линейном случае) при которой сумма квадратов отклонений всех точек от этой кривой минимальна. Для нахождения коэффициентов уравнения прямой a и b нужно решить систему уравнений, где xi (дата) и yi (курс евро) — данные из датасета:

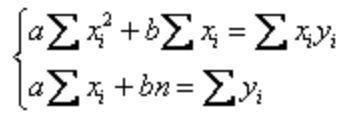
Сначала поле Date переведем в числовое поле, используя функцию DATEDIFF:

DATEDIFF(‘day’, {MIN([Date])}, [Date])

Это вычисление даст нам поле X. Форму графика мы не изменили — изменилась только размерность оси X, и новый график теперь начинается с нуля:

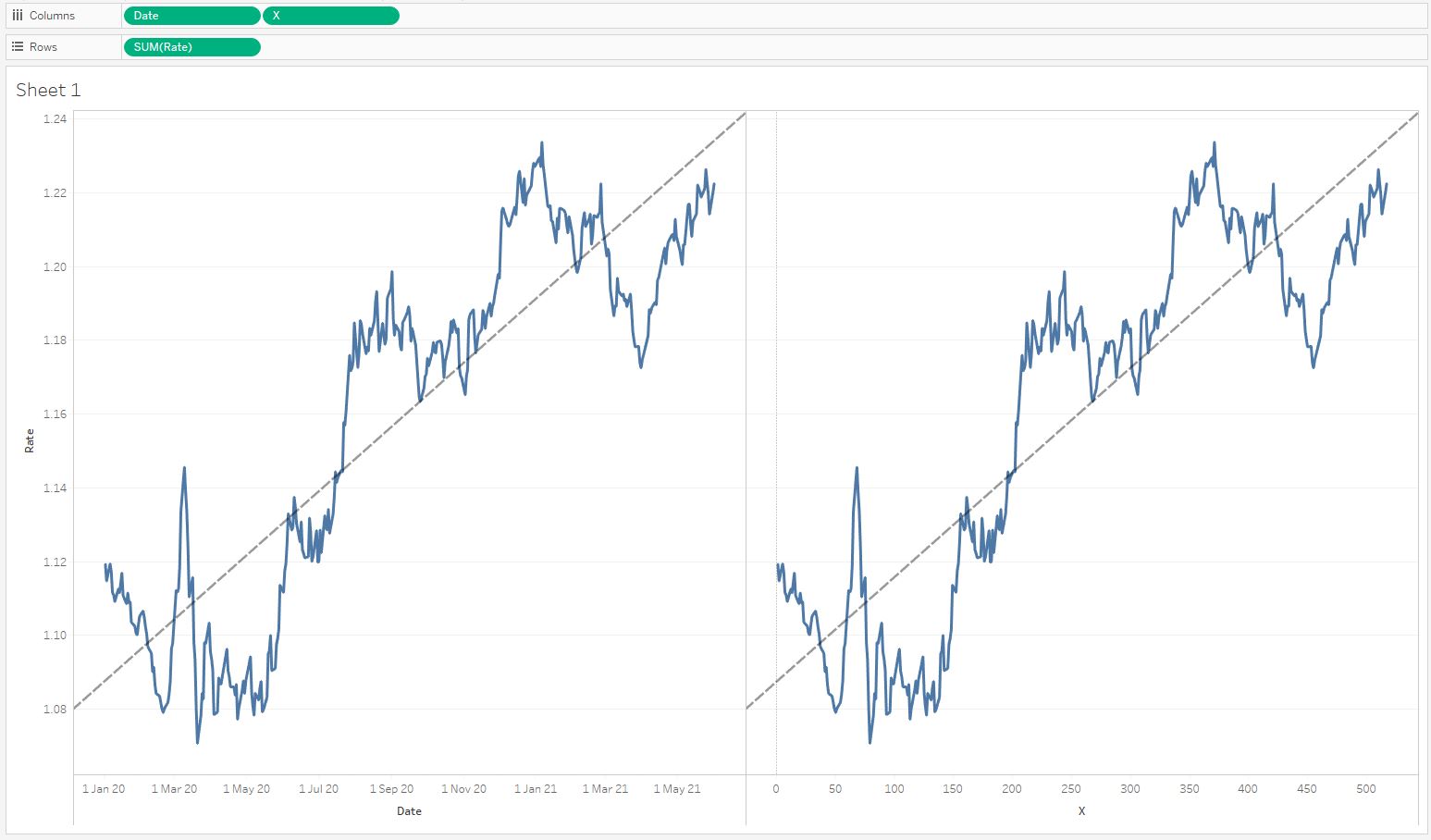
Решим системy уравнений методом Крамера, где Y — это поле Rate (курс евро):

Delta

SUM([X]^2)*COUNT([X]) — SUM([X])*SUM([X])

Delta A

SUM([X]*[Rate])*COUNT([X]) — SUM([X])*SUM([Rate])

Delta B

SUM([X]^2)*SUM([Rate]) — SUM([X]*[Rate])*SUM([X])

Коэффициенты A и B найдем следующим образом:

[Delta A] / [Delta]

[Delta B] / [Delta]

Итоговое уравнение прямой Y Regression:

{[A]}*[X] + {[B]}

Если построить графики для полей Rate и Y Regression, то получим неверную линию тренда (оранжевую) поскольку в данных есть пустые значения поля Rate — Null. Это объясняется тем, что по субботам, воскресеньям и праздникам торги не проходят, то есть, даты есть, а величин Y нет.

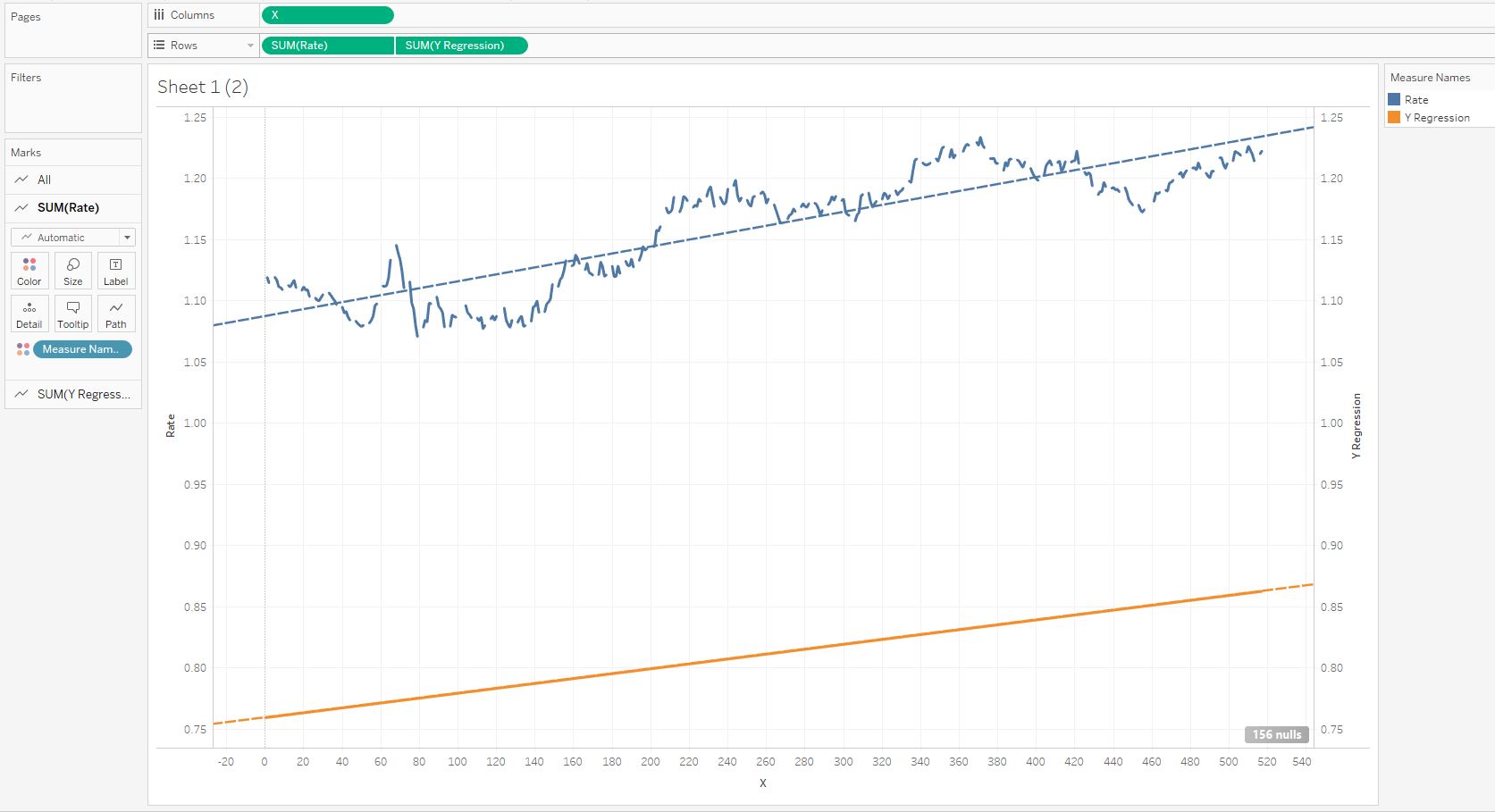
Если использовать входной фильтр Tableau, и для поля Rate оставить только Non-Null Values, то получим корректную картину:

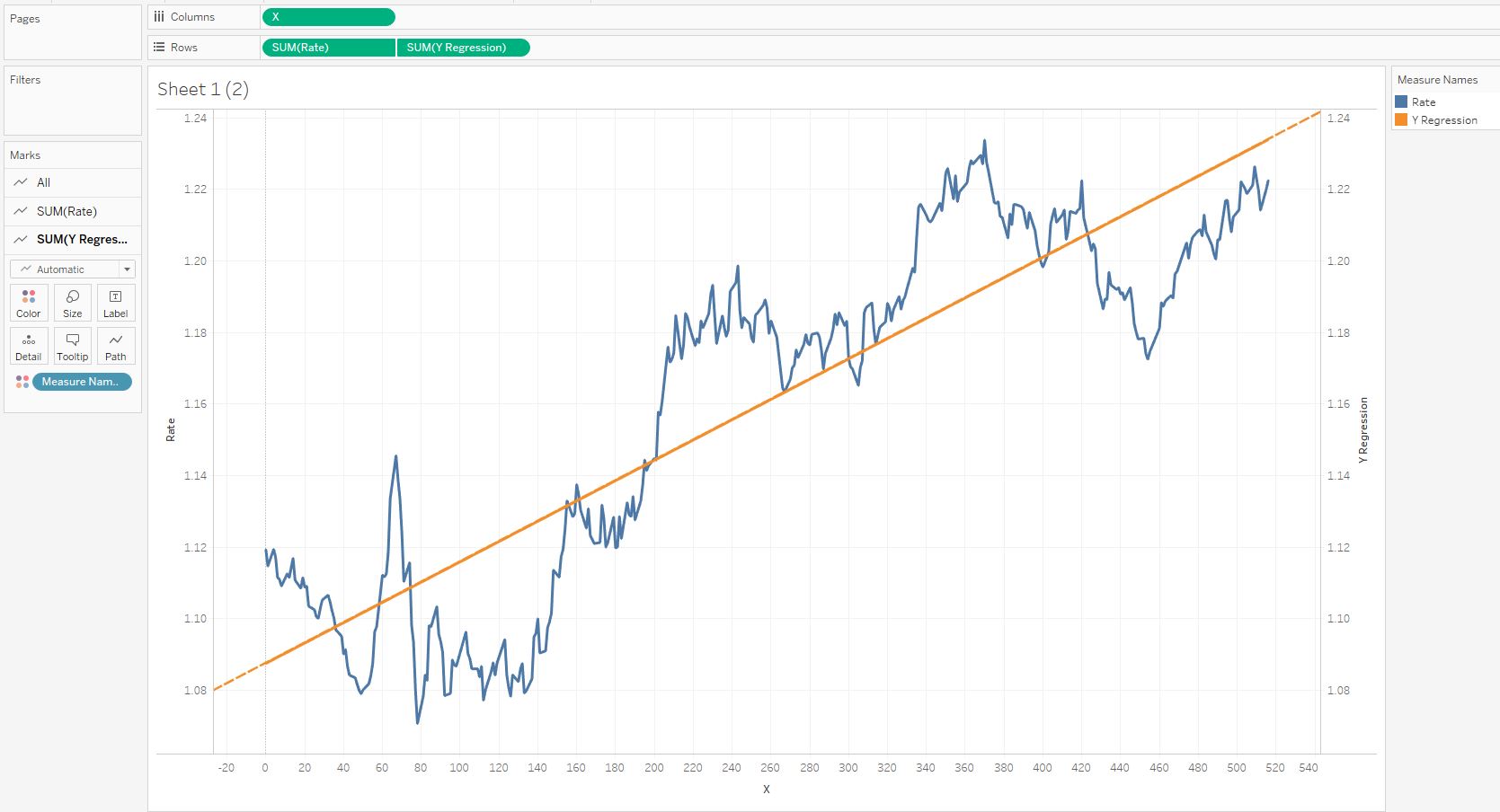
Оранжевая линия здесь и есть линия искомого тренда, уравнение для которой мы нашли. Вернем в Columns поле Date, и сравним синюю пунктирную линию тренда из меню Analysis Tableau и оранжевую жирную линию рассчитанного тренда. Они полностью совпадают:

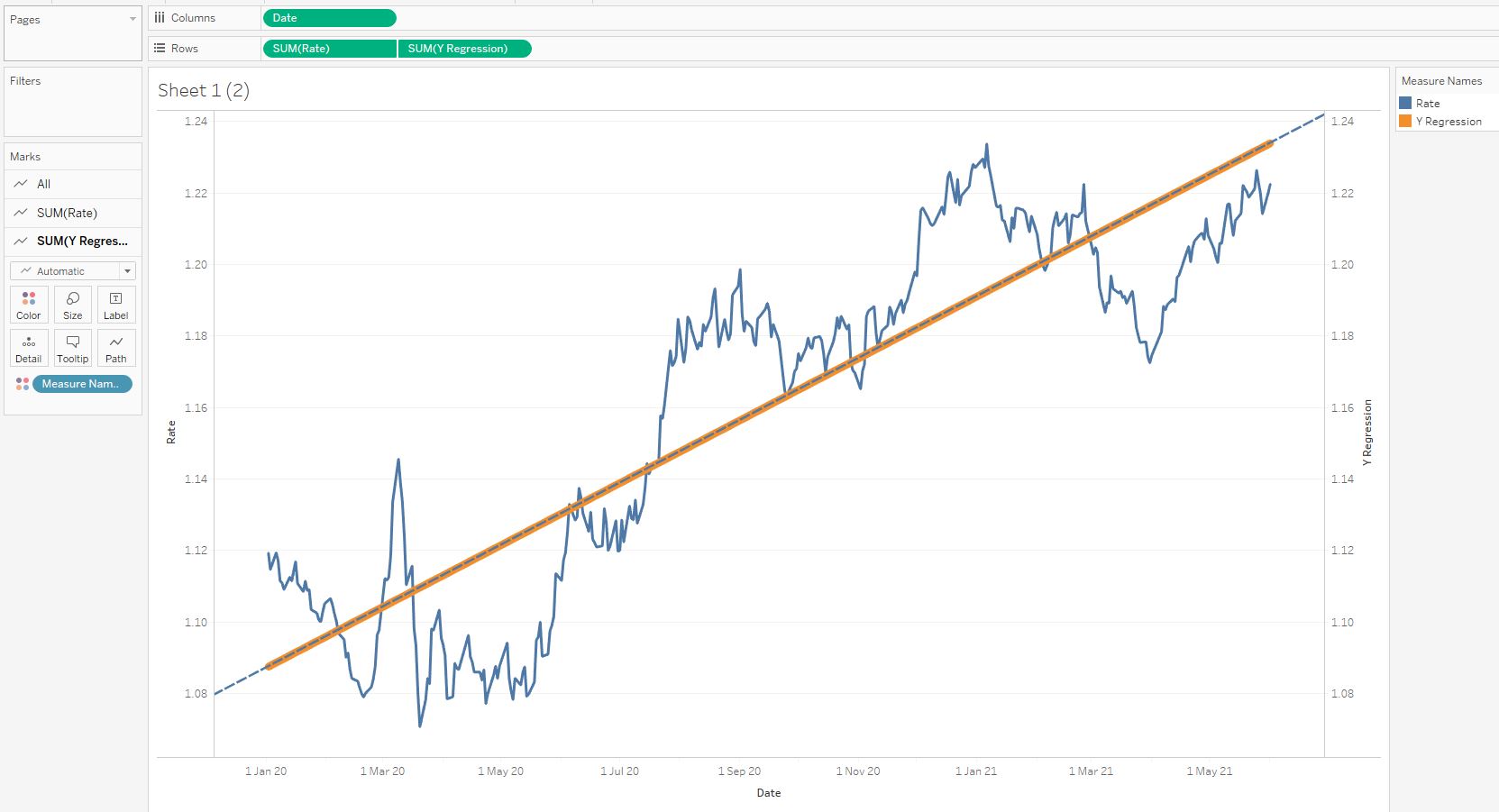
Мы нашли уравнение тренда y = ax + b. Коэффициенты a и b, полученные при помощи метода наименьших квадратов точно такие же, как и коэффициенты нативного метода Tableau. Коэффициент a определяется тангенсом угла наклона прямой, то есть, он отвечает за наклон прямой. Коэффициент b определяет сдвиг прямой отноcительно оси Y.

Итого, уравнение прямой у нас получилось следующее:

Rate = 0.000283748 * Date + 1.08751

Сравним данные Tableau:

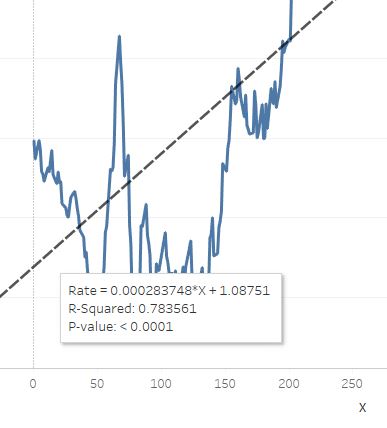
и рассчитанные нами коэффициенты a и b:

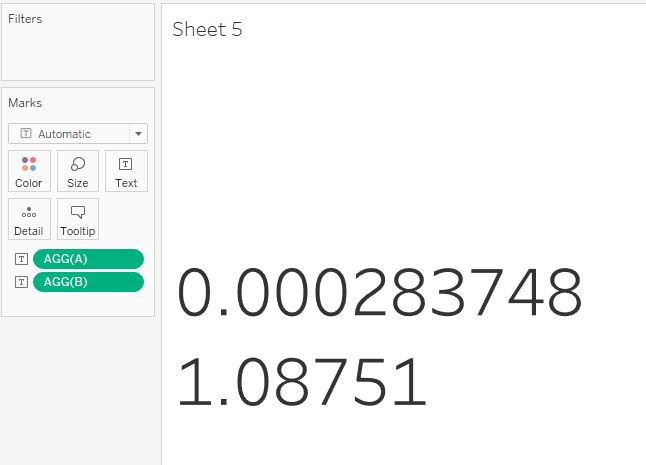
Они совершенно одинаковы. То есть, мы рассчитали уравнение прямой точно так же, как его рассчитало Tableau. Отдельно нужно обратить внимание на то, что коэффициенты b уравнения прямой для оси дат и оси X, приведенной к числам — разные.

Для дат b = -11.3497

Для чисел b = 1.08751

Это объяcняется тем, что при переводе дат в числа мы фактически сдвинули систему координат, поэтому поменялся коэффициент b. Угол наклона прямой при этом не поменялся — коэффициенты a одинаковы в обоих случаях, и направление тренда сохранилось.

Внимание: по выходным и праздникам биржи закрыты, поэтому в данных есть пробелы, они хорошо заметны на графиках. Линейный тренд мы построили не принимая во внимание выходные и праздники.

3. Расчет и визуализация отклонений

Уравнение тренда мы нашли, теперь попробуем визуально показать отклонения каждой точки относительно линии тренда. Для этого cделаем UNION с изначальной таблицей:

Создадим вычисление Variances:

CASE [Table Name]
WHEN ‘Sheet1’ THEN [Rate]
ELSE [Y Regression]
END

И нарисуем отклонения на графике:

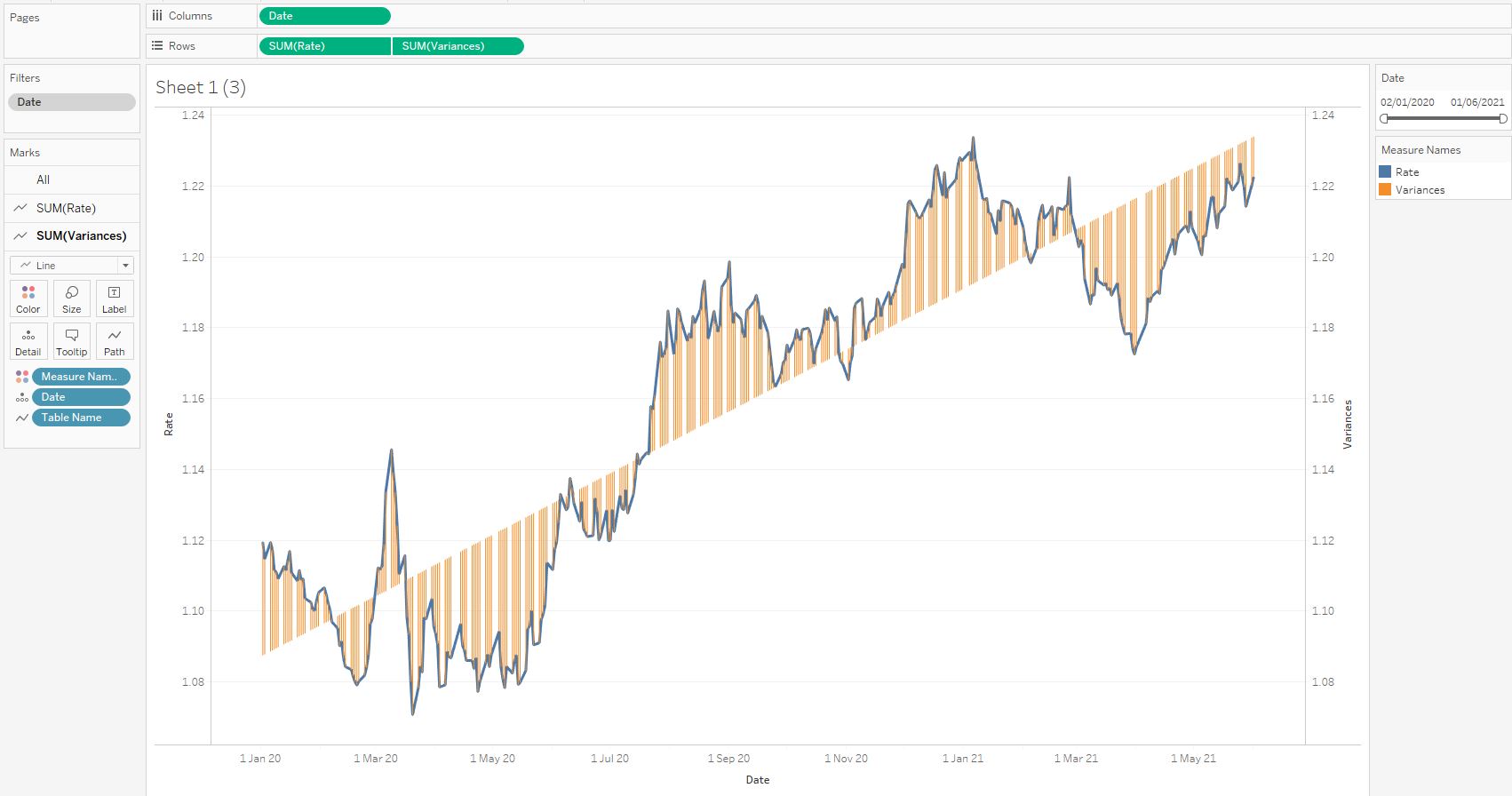
Если добавить контекстный фильтр Date, то сможем изменять диапазон дат графика. При изменениях фильтра коэффициенты a и b будут пересчитываться, и линии тренда на разных диапазонах дат будут разными.

Вертикальные линии помогают понять где данные отсутствуют, поскольку на обычном линейном графике этого не видно. Также визуально можно оценить отклонения курса EUR/USD относительно линии тренда.

Отклонение относительно линии тренда определяется выражением:

[Rate] — [Y Regression]

Добавив это вычисление в текст и цвет, получим следующую картину с отклонениями, где довольно просто видеть волны курса и отклонения относительно линии тренда:

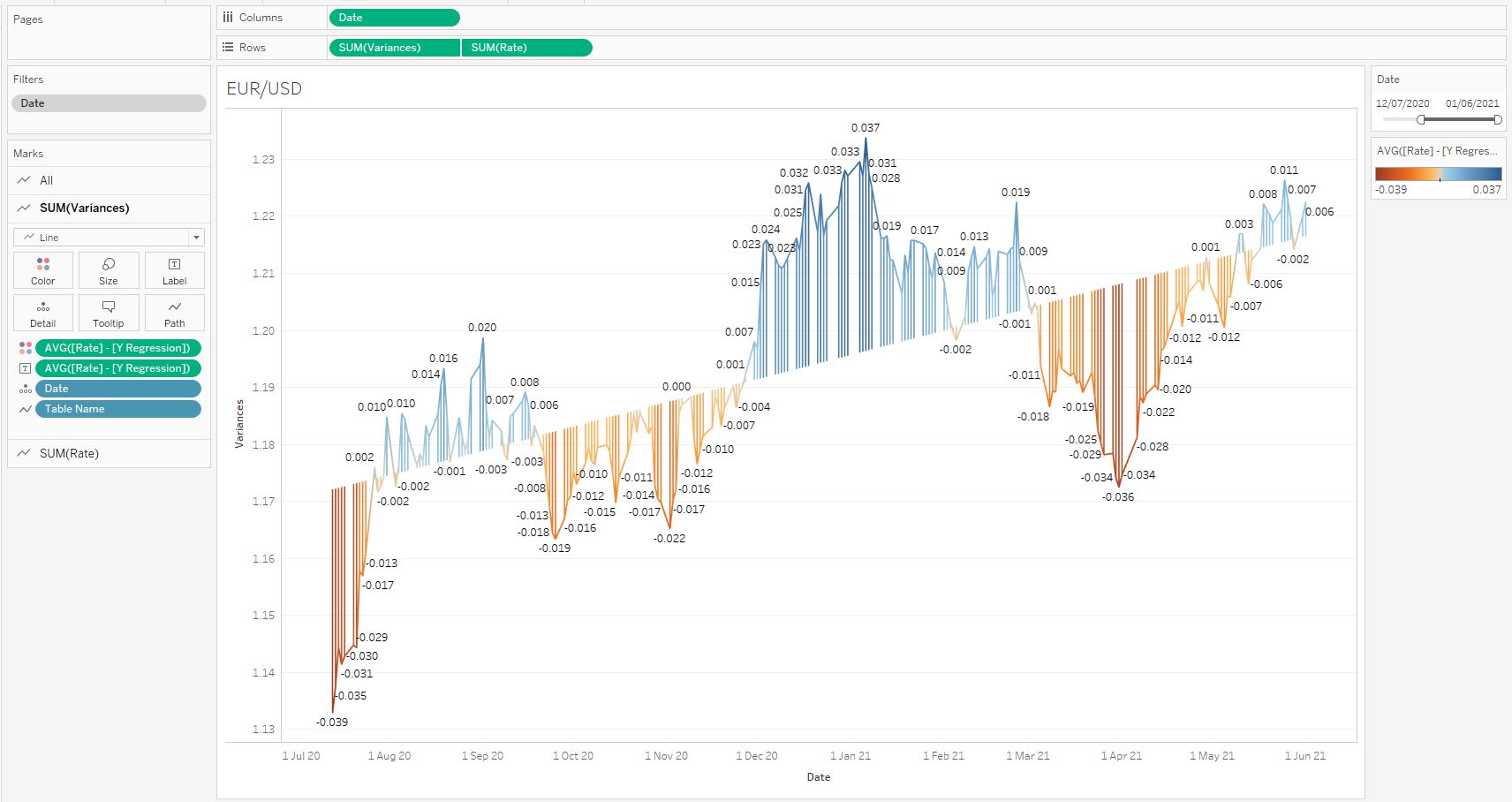
4. Ковариация

Если между двумя переменными существует линейная связь, то есть, при изменении одной величины линейно изменяется другая, то говорят, что между переменными существует линейная корреляция. Далее рассмотрим величины для оценки силы корреляции.

Ковариация — это мера линейной зависимости двух величин. Ковариацией является средняя величина произведений отклонений значений от средних значений соответствующих выборок:

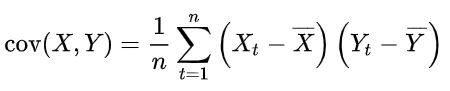
Cредние значения выборок (также называемые выборочными средними) определяют по формулам:

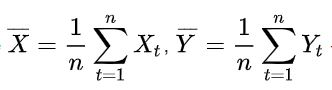
Рассчитаем их в Tableau:

Mean X

{ FIXED: AVG([X])}

Mean Y

{ FIXED: AVG([Rate])}

Выражение для коэффициента ковариации Covariance:

{FIXED: SUM(([X] — [X Mean])*([Rate] — [Y Mean]))}
/
({FIXED: COUNTD([X])} -1)

В Tableau существует функция COVAR для расчета коэффициента ковариации. Рассчитаем коэффициент Covariance COVAR при помощи этой функции:

{CORR([X], [Rate])}

Сейчас можем рассчитывать величину ковариации для любого диапазона дат. Cравним значения коэффициентов, полученных разными путями:

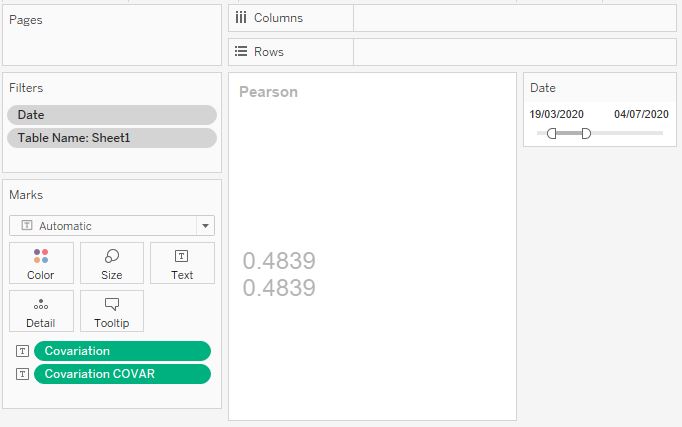
Коэффициент ковариации отражает степень корреляции переменных, он может быть как положительным (отражает прямую корреляцию), так и отрицательным (для обратной корреляции).

Проблема этой величины в том, что по её абсолютному значению невозможно оценить насколько сильно связаны переменные. Для этого значение ковариации нормируют, поделив её на произведение среднеквадратических отклонений. Полученная величина называется коэффициентом линейной корреляции Пирсона.

5. Коэффициент линейной корреляции Пирсона

Коэффициент линейной корреляции Пирсона является наверное самой известной мерой оценки величины линейной корреляции.

Давайте создадим вычисление Pearson CORR:

{CORR([X], [Rate])}

Функция CORR в Tableau возвращает коэффициент Пирсона. Фигурные скобки здесь обусловлены тем, что нам нужно взять все значения по оси дат и сосчитать одно значение коэффициента. Запись вычисления эквивалентна следующей записи:

{FIXED: CORR([X], [Rate])}

Поскольку функция CORR работает только с агрегациями, она будет агрегировать значения на уровнях гранулярности, выбранных в Tableau. То есть, если просто сосчитать CORR([X], [Rate]) для каждой точки на графике, это даст неверные результаты, так как в каждой агрегации будет только одно значение. Поэтому мы используем функцию FIXED.

Обычно люди плохо представляют как работает коэффициент Пирсона и какие вычисления используются внутри Tableau для его расчета. Поэтому сейчас разберемся в этих вычислениях. Формула для вычисления коэффициента Пирсона следующая:

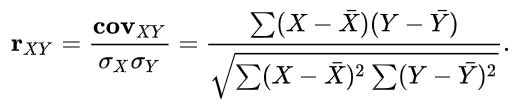
Выражения:

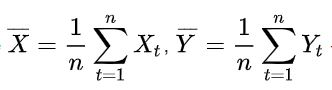
— это средние суммы выборок, которые рассчитаем в Tableau следующим образом:

Mean X

{ FIXED: AVG([X])}

Mean Y

{ FIXED: AVG([Rate])}

Сам коэффициент Пирсона рассчитывается так:

Pearson

{FIXED: SUM(([X] — [X Mean])*([Rate] — [Y Mean]))}
/
{FIXED: SQRT(SUM(([X] — [X Mean])^2)*SUM(([Rate] — [Y Mean])^2))}

Теперь давайте сравним вычисления CORR и вычисления, которые мы привели выше на разных диапазонах дат. Cделаем контекстный фильтр, выберем любой диапазон и убедимся, что значения эквивалентны:

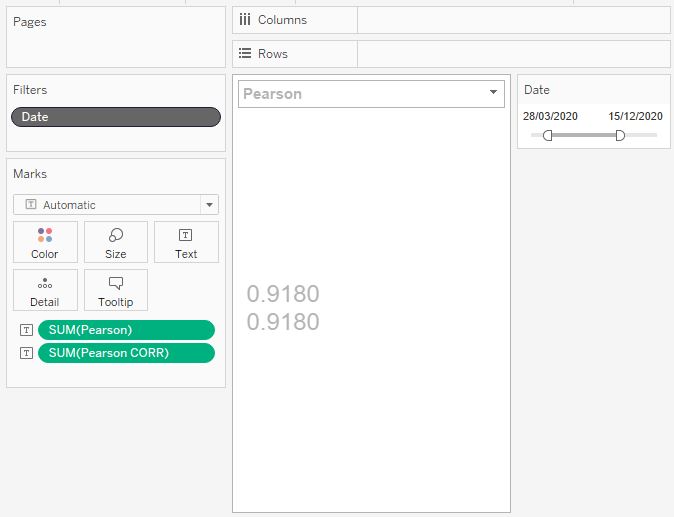
Коэффициент Пирсона может принимать значение от -1 до 1. Знак минус означает обратную (отрицательную) корреляцию, положительное значение коэффициента означает прямую (положительную корреляцию). Чем ближе значения коэффициентов к единице по модулю, тем сильнее степень корреляции.

Курс евро к доллару на выбранном интервале неуклонно рос, поэтому имеем сильную прямую корреляцию.

6. Сила коэффициента корреляции. Шкала Чеддока

Мы выяснили, что коэффициент корреляции Пирсона изменяется от -1 до 1, однако довольно сложно навскидку сказать когда корреляция сильная, а когда — нет. Для этого вводятся некоторые соглашения перевода числовой метрики (continious measure) в категории (quantitative measure) для более понятного восприятия человеком.

Рассмотрим шкалу Чеддока (Chaddock scale), которая разбивает интервал от 0 до 1 для прямой корреляции и интервал от -1 до 0 на несколько категорий:

Количественная мера тесноты связи	Качественная характеристика силы связи
0.9 to 1 (-0.9 to -1)	Весьма высокая
0.7 to 0.9 (-0.7 to -0.9)	Высокая
0.5 to 0.7 (-0.5 to -0.7)	Заметная
0.3 to 0.5 (-0.3 to -0.5)	Средняя
0.1 to 0.3 (-0.1 to -0.3)	Слабая

Size of Correlation	Interpretation
0.9 to 1 (-0.9 to -1)	Very high positive (negative) correlation
0.7 to 0.9 (-0.7 to -0.9)	High positive (nеgative) correlation
0.5 to 0.7 (-0.5 to -0.7)	Salient positive (negative) correlation
0.3 to 0.5 (-0.3 to -0.5)	Moderate positive (negative) correlation
0.1 to 0.3 (-0.1 to -0.3)	Weak correlation

Такая шкала встречается в различных научных работах (1, 2) с незначительными отличиями.

Я для себя интерпретирую коэффициент Пирсона так: меньше 0.25 — нет корреляции, больше 0.75 — высокая корреляция, от 0.25 до 0.75 — средняя корреляция. Это вполне достаточно чтобы быстро понять есть линейная корреляция между переменными или нет.

Далее мы будем руководствоваться шкалой из таблицы. Давайте построим такую шкалу в Tableau. Для этого создадим датасет из таблицы в Excel и подключим к нему Tableau:

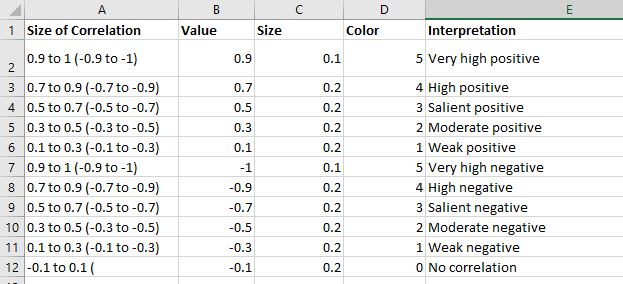
Саму шкалу сделаем в виде вертикальной диаграммы Ганта, где поле Size — это высота деления, а поле Color создаст изменение цвета шкалы:

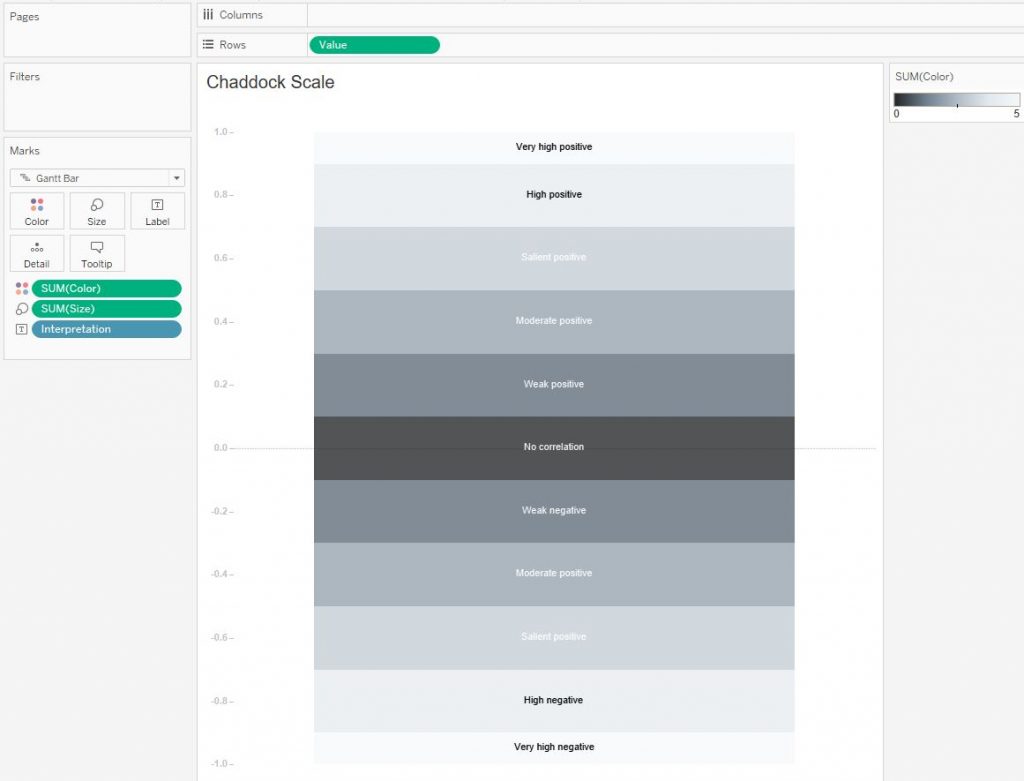
Сделаем индикатор, который будет показывать значение коэффициента Пирсона на шкале:

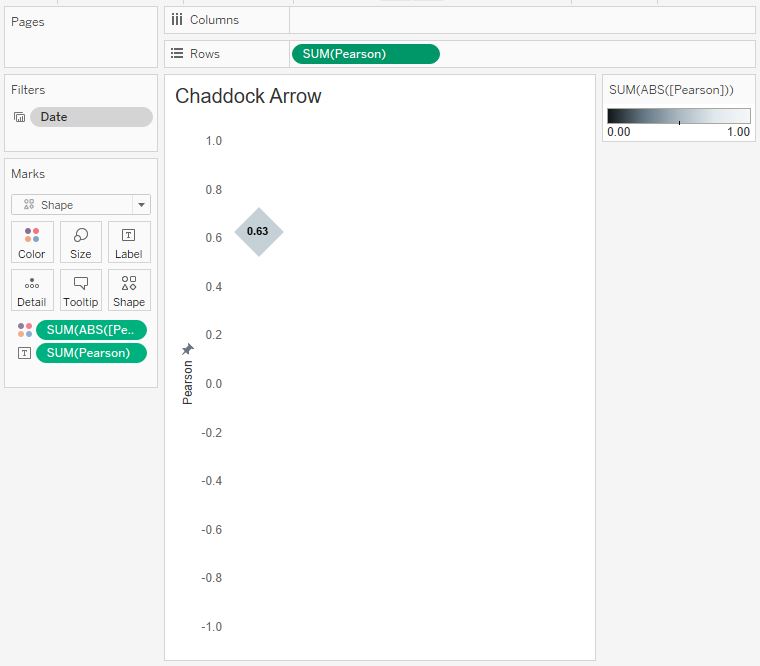
После этого оба листа поместим в один плавающий контейнер и добавим Show/Hide Button для того чтобы скрывать и показывать шкалу Чеддока:

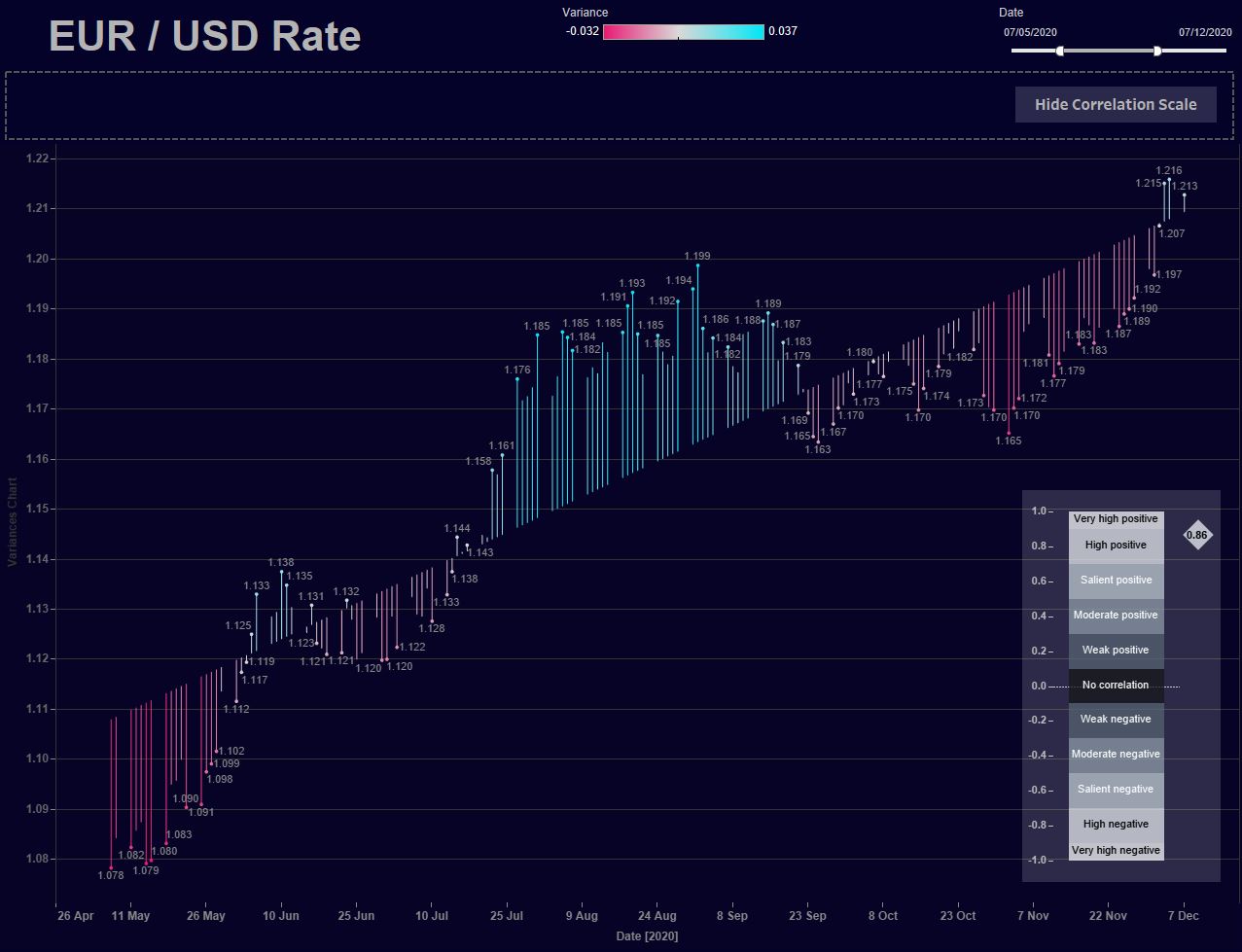
Теперь при изменении диапазона дат будет рассчитываться коэффициент Пирсона и указатель на шкале будет сдвигаться, показывая степень корреляции.

7. Коэффициент детерминации R²

Следующим параметром, который мы найдем при помощи вычислений Tableau, будет коэффициент детерминации R²(R-Squared). Этот параметр Tableau вычисляет нативно при построении линии тренда. Для нашего случая на всем диапазоне дат он равен:

R-Squared: 0.783561

Коэффициент детерминации отражает долю дисперсии зависимой переменной (курса Евро в нашем случае).

Рассчитаем его по формуле:

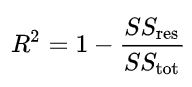
где SS_res — это сумма квадратов отклонений от линии тренда (residual sum of squares), SS_tot — общая сумма квадратов (total sum of squares) или сумма квадратов отклонения от математического ожидания (среднего значения). Эти две величины графически объясняются следующим рисунком, на котором сумма квадратов ошибок характеризует отклонение всех точек от линии тренда, а общая сумма квадратов отражает отклонение всех точек от общего среднего значения:

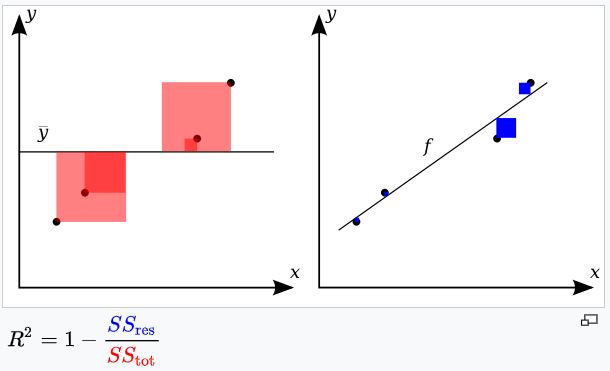
Формулы для этих величин следующие:

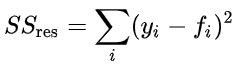f здесь — это функция линейного тренда, мы ее считали выше.

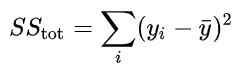Создадим вычисления в Tableau:

Residual Sum of Squares

{ FIXED: SUM(([Rate] — [Y Regression])^2)}

Total Sum of Squares

{ FIXED: SUM(([Rate] — [Mean Y])^2)}

Вычисление для R2:

1 — [Residual Sum of Squares] / [Total Sum of Squares]

Значение R2 теперь можно отображать в Tableau на любом диапазоне дат:

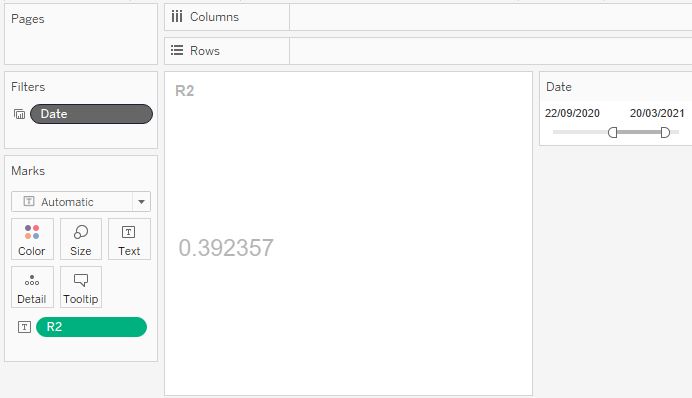
Коэффициент детерминации принимает значения от 0 до 1.

И самое важное: Коэффициент детерминации — это коэффициент Пирсона в квадрате.

8. Финальная визуализация

В финальной визуализации я вынес все рассчитываемые статистические метрики и функцию тренда отдельными листами с текстом. Также сделал параметры Chart Type и Text Marks. Первый параметр позволяет выбирать типы отображения графика курса евро и линии тренда, а второй параметр определяет какие значения будем показывать на графике текстом.

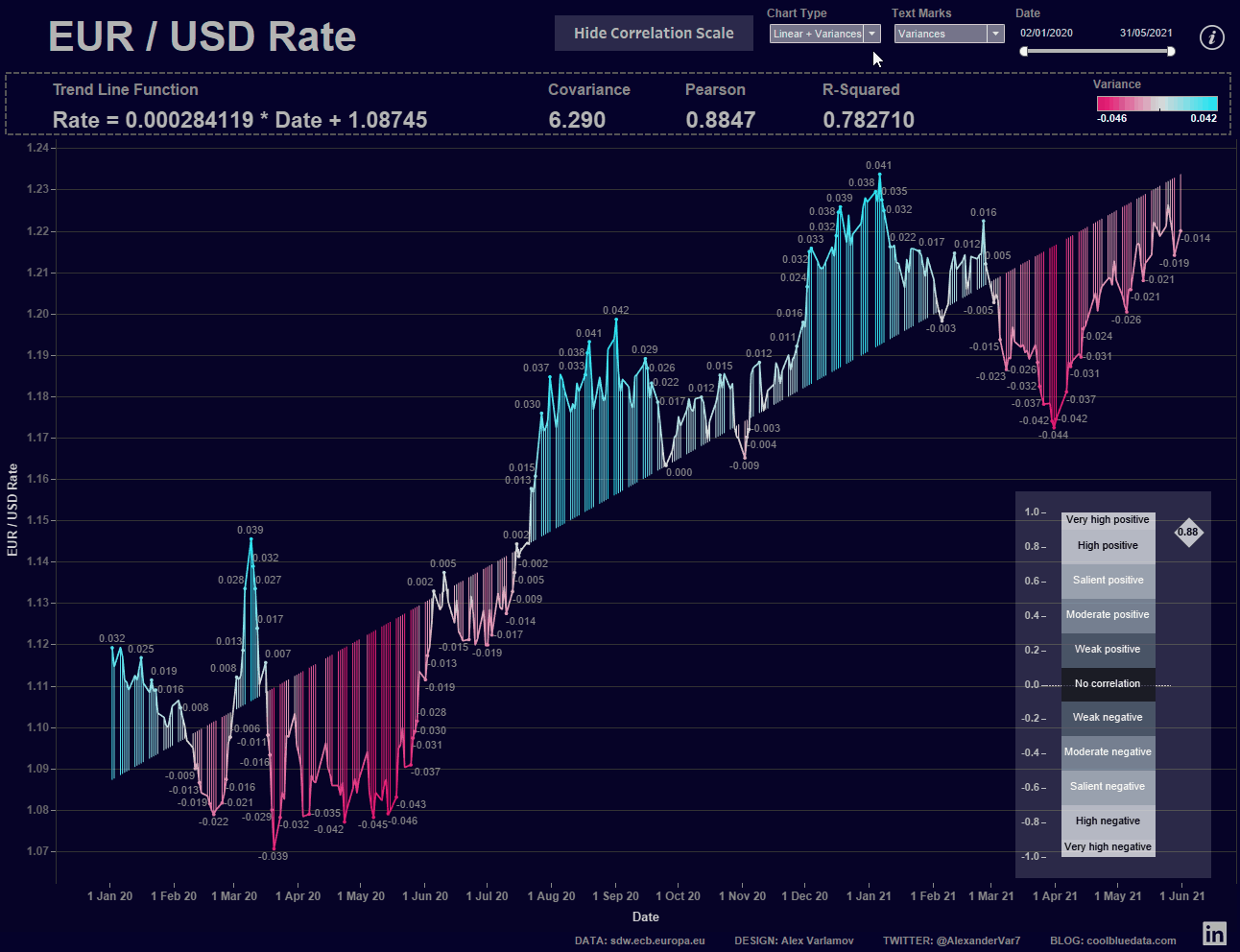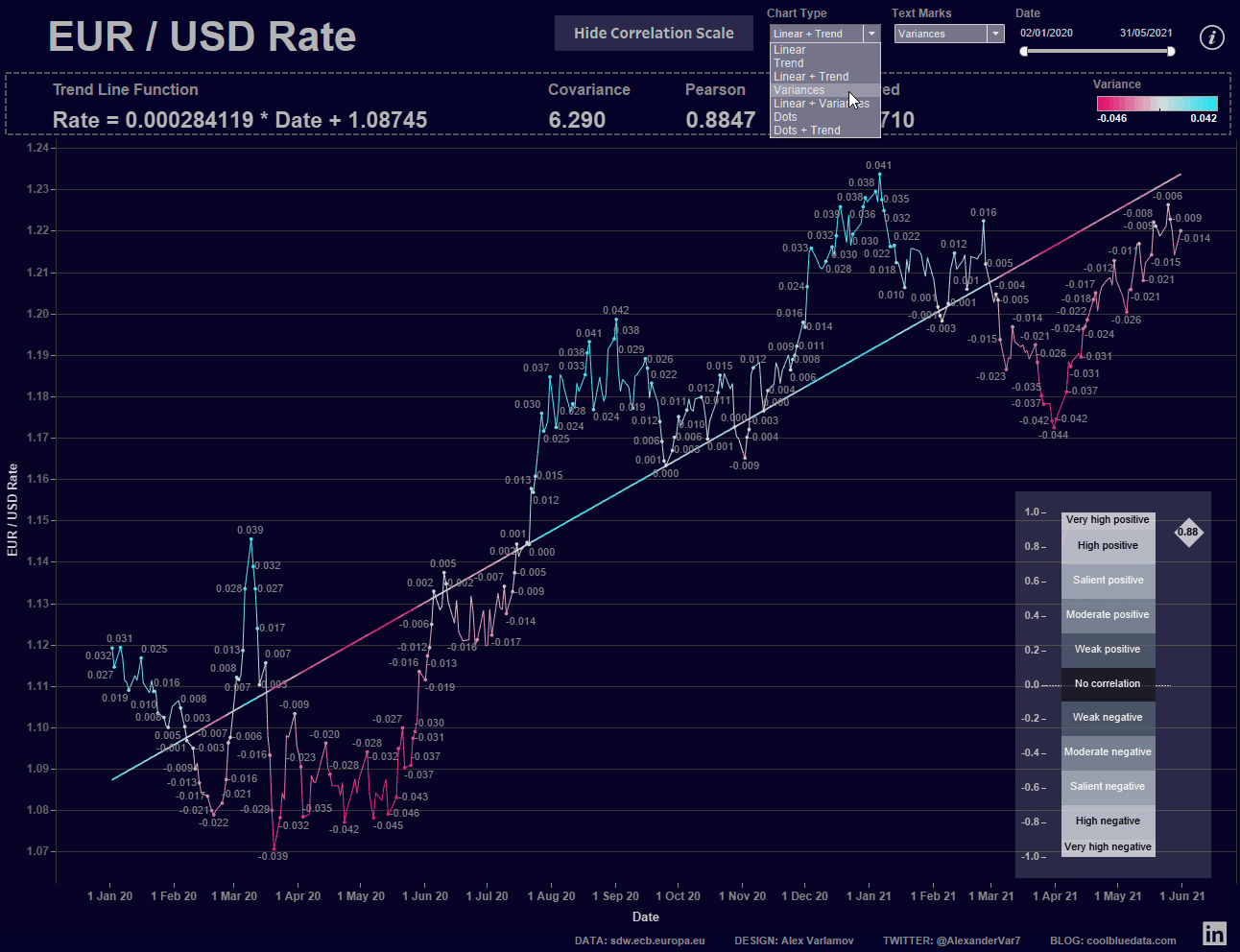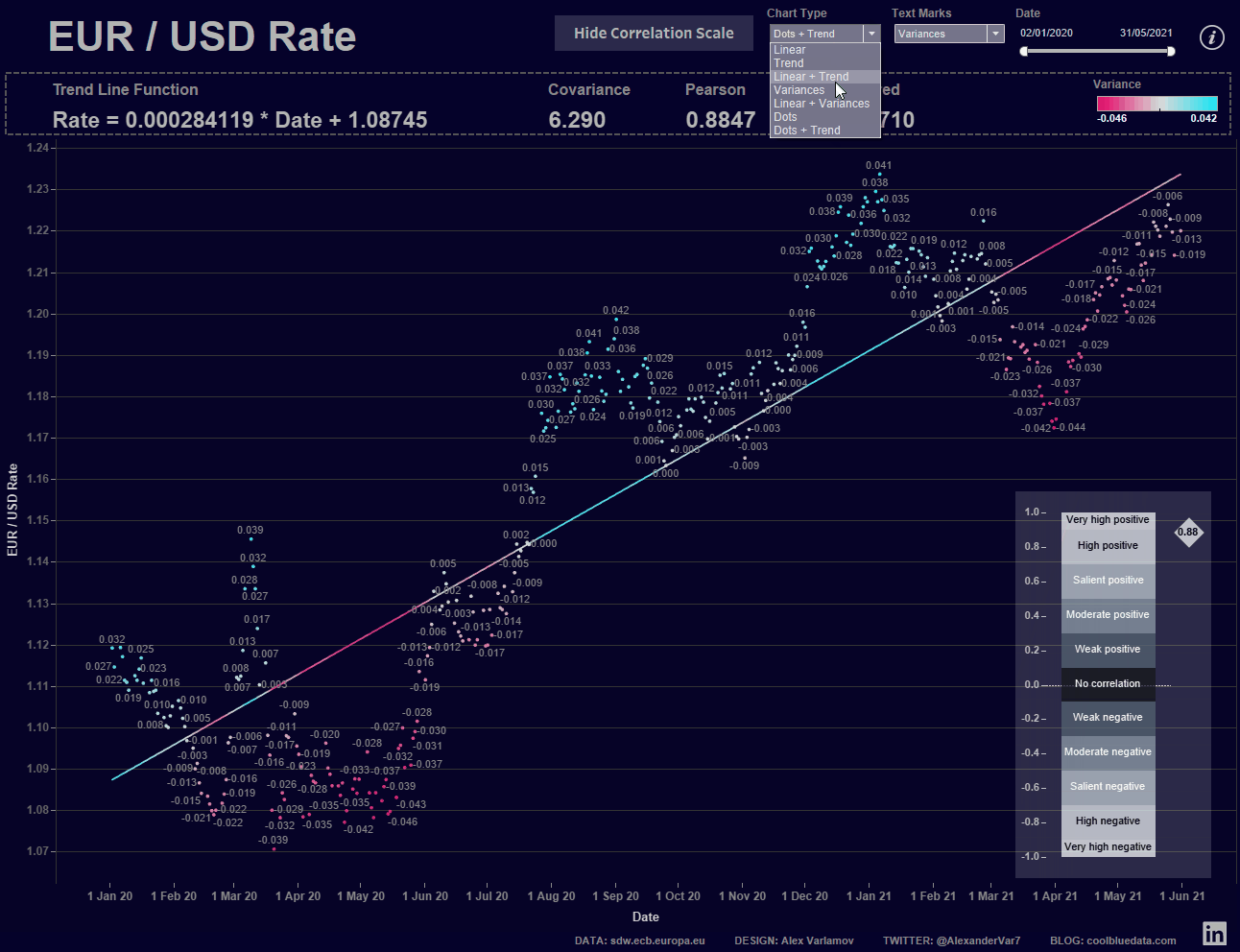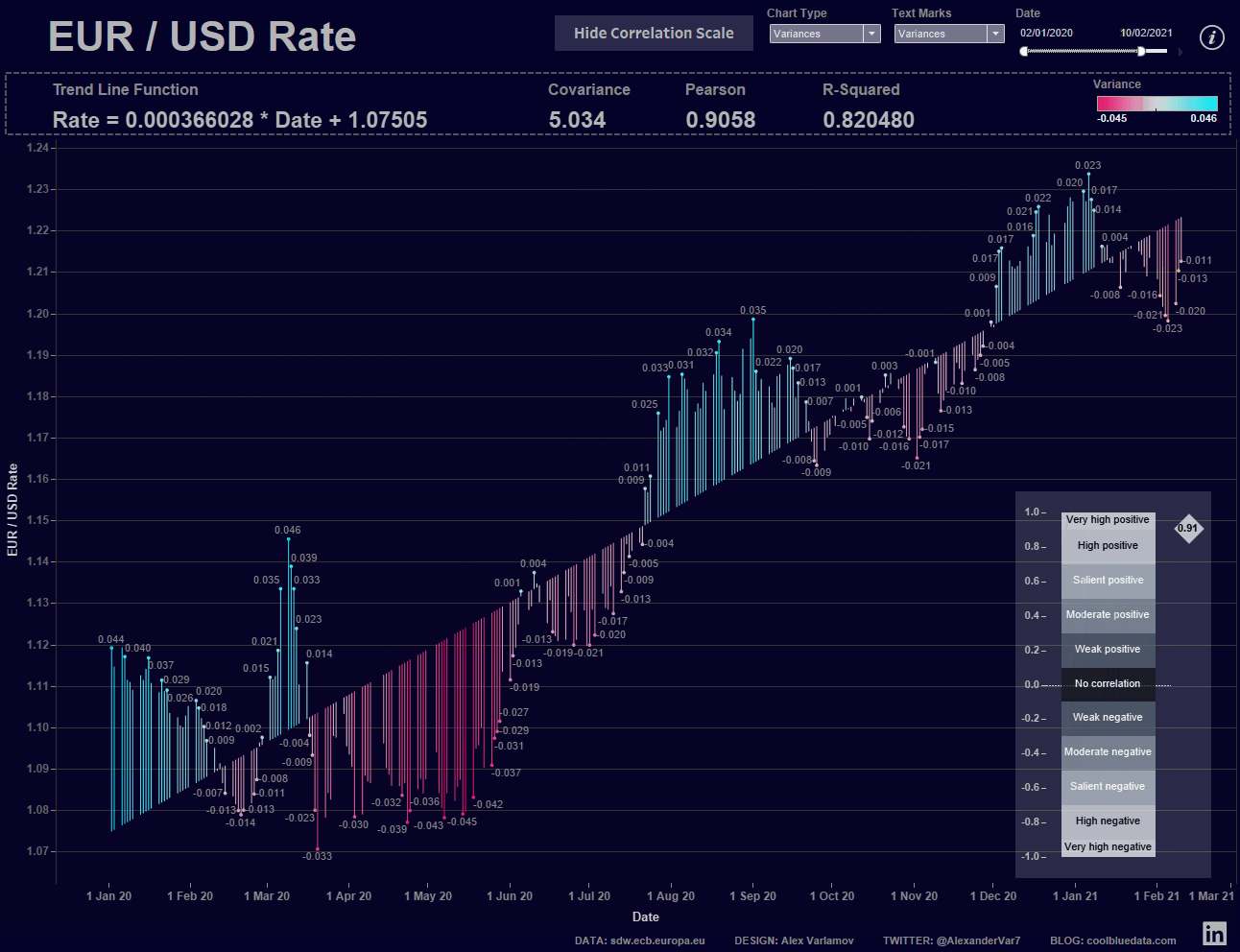
Ценность такой визуализации в том, что меняя диапазон дат вы увидите изменения трендов и статистических параметров, а по шкале Чеддока вы можете сопоставить вид тренда и значение коэффициента Пирсона, то есть, на самом графике увидите силу корреляции между курсом евро и временем.

9. Сравнение четырех способов вычисления коэффициента Пирсона

Коэффициент Пирсона можно найти как минимум четырьмя способов в Tableau:

Построить линию тренда, взять квадратный корень из R-Squared
Вычислить коэффициент Пирсона через общие математические формулы как было показано выше
Рассчитать коэффициент Пирсона через функцию CORR
Найти коэффициент Пирсона через функцию WINDOW_CORR

1. Первый путь: cтроим линию тренда нативно, R-Squared = 0.783561. Его рассчитало Tableau по своей внутренней логике. Берем квадратный корень из этого числа, получаем 0.885193.

Здесь надо учитывать что при отрицательной корреляции знака «минус» мы не получим.

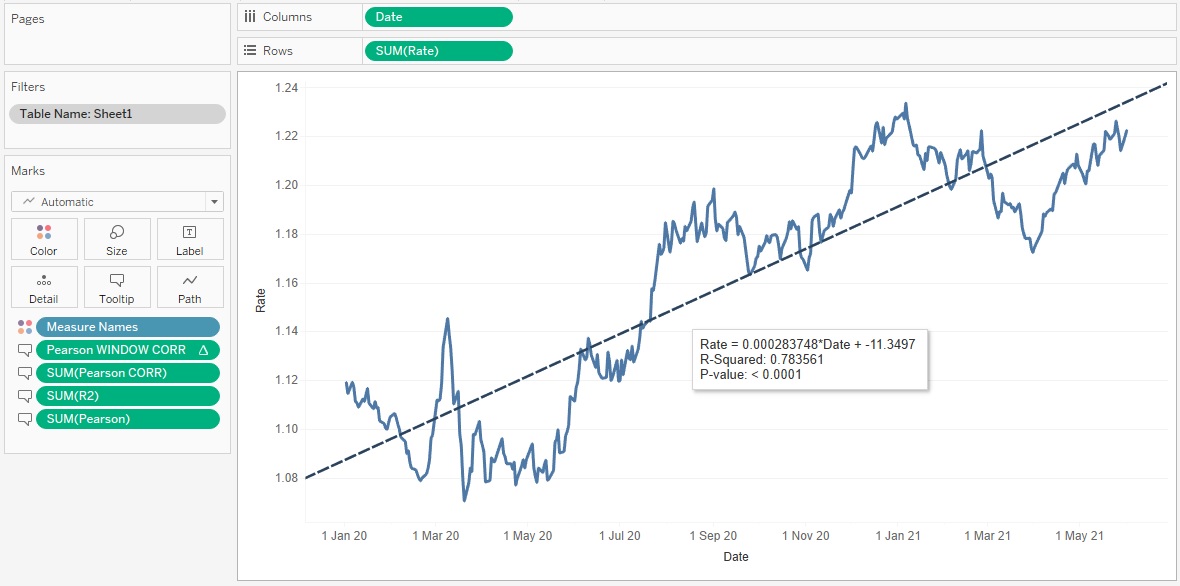
2. Второй путь был описан выше, он базируется на математических формулах. Это вычисление Pearson, я вынес его в тултип на скриншоте ниже. Коэффициент равен 0.885190

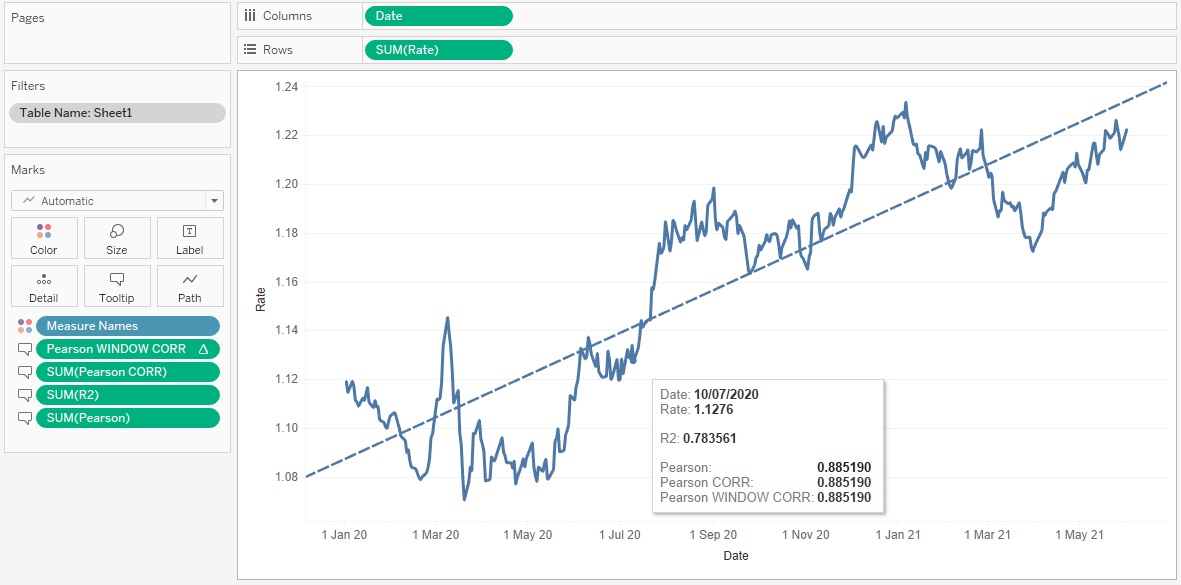
3. Третий путь тоже был упомянут в статье. Он использует функцию CORR для вычисления коэффициента:

{FIXED: CORR([X], [Rate])}

Вычисление также вынесено в тултип как Pearson CORR, его значение равно 0.885190

4. Четвертый путь вычисления коэффициента базируется на табличном вычислении WINDOW_CORR, которое проходится по всем точкам выборки и возвращает коэффициент корреляции Пирсона:

WINDOW_CORR(SUM([X]), SUM([Rate]))

Это вычисление вынесено в тултип как Pearson WINDOW_CORR, его значение равно 0.885190

В итоге все 4 вычисления сошлись. Погрешность в 6-ом знаке после запятой первого метода объясняется тем, что R-Squared еще числа после шестого знака, которые мы не учли.

Заключение

В бизнесе очень важно следить за тенденциями изменения различного рода метрик во времени. Одним из методов количественной оценки тенденций является регрессионный анализ, то есть, поиск некоторой функции, описывающей поведение метрики во времени.

В этой статье мы рассмотрели формулы вычисления базовых метрик линейной регрессии, а также показали альтернативные методы визуализации временных трендов. Кроме этого, мы визуализировали шкалу Чеддока, на которой можно видеть силу корреляционной связи двух переменных.

Вычисления в статье базировались на функциях Level of Details (FIXED), однако можно использовать функции CORR, COVAR или табличные вычисления (WINDOW_CORR, WINDOW_COVAR), как было показано в последнем пункте.

В статье не были рассмотрены доверительные интервалы и p-значения, но эти метрики тоже важны для регрессионного анализа, и Tableau может их строить нативно. Линейной регрессии в некоторых случаях недостаточно для понимания трендов, поэтому пользуются другими типами (например, экспоненциальная или полиномиальная регрессии).

Следующая статья «Линейная регрессия в Tableau. Часть 2, Группы» рассказывает о нахождении функций и построении линий регрессии групп данных, а также создании инструмента для изучения влияния одних переменных на другие.